418341 ภาคต้น 2552/โจทย์ปัญหาอัลกอริืทึมเกี่ยวกับกราฟ
เนื้อหา
ข้อ 1
ในชั้นเรียนเราได้พูดถึงการเก็บ undirected graph ด้วย adjacency matrix และ adjacency list
ถ้าเราจะเก็บ directed graph ด้วย adjacency matrix และ adjacency list บ้าง จะต้องเปลี่ยนแปลงรูปแบบการจัดเ็ก็บอย่างไรบ้าง?
ข้อ 2
[Dasgupta, Papadimitriou, Varizari 3.5] กำหนดกราฟแบบมีทิศทาง มาให้ กราฟผันกลับ (reverse) ของ คือกราฟ โดยที่มีเซตของ vertex เป็นเซตเดียวกันแต่ edge ใน คือ edge ใน ที่ถูกกลับข้าง (กล่าวคือ )
จงออกแบบอัลกอริทึมที่เมื่อให้ ในรูปแบบ adjacency list ให้คำนวณ ในรูปแบบ adjacency เช่นกัน อัลกอริทึมของคุณควรจะทำงานได้ในเวลา
ข้อ 3
- [Kleinberg & Tardos 3.2] จงออกแบบอัลกอริืทึมที่ตรวจสอบว่า undirected garph ที่ให้มาในรูปแบบ adjacency list มี cycle หรือไม่ ถ้ามีให้พิมพ์ออกมาหนึ่ง cycle (วงไหนก็ได้) อัลกอริึทึมของคุณควรจะทำงานได้ในเวลา เมื่อ คือจำนวน vertex คือจำนวน edge
- [Dasgupta, Papadimitriou, Vazirani 3.11] จงออกแบบอัลกอริทึมที่ เมื่อให้ directed graph และให้ edge มา แล้วคำนวณว่ามี cycle ที่มี เป็น edge หนึ่งอยู่ีใน cycle นั้นหรือไม่ ถ้ามีให้พิมพ์ออกมาสักหนึ่ง cycle อัลกอริทึมของคุณควรจะทำงานได้ในเวลา
ข้อ 4
สมมติว่าเราอัลกอริทึมในการทำ depth first search ให้สร้างอะเรย์ขนาด ช่อง เมื่อ คือจำนวน vertex เพิ่มขึ้นอีกสองอะเรย์ ได้แก่ และ โดยมีตัวแปร global ชื่อ clock ซึ่งมีค่าเริ่มแรกเท่ากับ 1 เป็นตัวช่วย ดังต่อไปนี้
<geshi lang="c"> DFS(u) {
pre[u] = clock
clock = clock + 1
explored[u] = 1
for i = 1 to d[u] do
{
v = a[u][i]
if explored[v] = 0 then
{
parent[v] = u
DFS(v)
}
}
post[u] = clock clock = clock + 1
} </geshi>
กล่าวคือ เป็นเหมือนเวลาที่ DFS(u) เริ่มทำงาน และ เป็นเวลาที่ DFS(u) ทำงานเสร็จ
นอกจากนี้ในการทำ depth first search เราจะพยายามเรียก DFS(u) ที่ทุก vertex u ในกราฟหามันยังไม่เคยถูกไปถึงด้วย DFS มาก่อน ดังต่อไปนี้
<geshi lang="c"> DFSALL() {
for u = 1 to n do
if explored[u] = 0 then
{
parent[u] = 0
DFS(u)
}
} </geshi>
ข้อย่อย 4.1
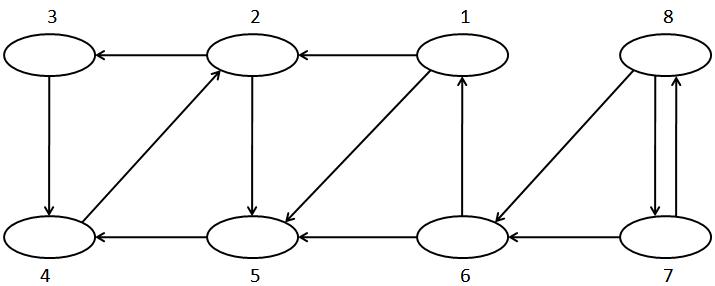
พิจารณากราฟแบบมีทิศทางข้างล่างนี้
จงรัน DFSALL บนกราฟข้างบน โดยเวลาไล่ vertex ให้ไล่จาก vertex ที่มีหมายเลขน้อยไปยังมากหมายเลขมาก (ยกตัวอย่างเช่น vertex ที่มี edge พุ่งออกจาก 7 ไปถึง ได้แก่ vertex 6 และ 8 เป็นต้น) แล้วเขียน
- DFS tree
- อะเรย์
- อะเรย์
- อะเรย์
ข้อย่อย 4.2
หากเราจำแนก edge ในกราฟข้างบนออกเป็น 4 ประเภท ตังต่อไปนี้
- Tree edge คือ edge ที่อยู่บน DFS tree ที่ได้จากการทำ DFS
- Back edge คือ edge ที่พุ่งออกจาก vertex ไปหาบรรพบุรุษของมันใน DFS tree
- Forward edge คือ edge ที่พุ่งออกจาก vertex ไปหาลูกหลานของมันใน DFS tree
- Cross edge คือ edge อื่นๆ ที่ไม่เข้าพวกทั้งสามข้างต้น
แล้วจงบอกว่า edge ในกราฟเป็น edge แต่ละ edge เป็น edge ชนิดใดบ้าง
ข้อย่อย 4.3
ให้ เป็นกราฟแบบมีทิศทาง สมมติว่าเรารัน DFSALL บน แล้ว จงพิสูจน์ "สมบัติวงเล็บ" ต่อไปนี้:
ถ้า และ เป็น vertex สอง vertex ใดๆ ในกราฟแล้ว ภายในข้อเท็จจริงสามข้อต่อไปนี้ จะมีข้อเท็จจริงข้อหนึ่งเป็นจริง และมันจะเป็นจริงเพียงข้อเดียวเท่านั้น
- ช่วง และช่วง ไม่มีสมาชิกร่วมกันเลย
ข้อย่อย 4.4
จงพิสูจน์ว่า สำหรับ edge ใดๆ เราสามารถใช้สมบัติวงเล็บข้างต้นในการจำแนกประเภทของมันได้
- ถ้า แล้ว ต้องเป็น tree edge หรือ forward edge
- ถ้า แล้ว ต้องเป็น back edge
- ถ้า และ ไม่มีส่วนร่วมกัน แล้ว ต้องเป็น cross edge
ข้อย่อย 4.5
ถ้าเรารัน DFSALL บน undirected graph แทนที่จะเป็น directed graph แล้ว จงพิสูจน์ว่าจะไม่มี forward edge หรือ cross edge อยู่เลย (กล่าวคือ edge ทุก edge จะเป็น tree edge หรือ back edge เท่านั้น)
ข้อ 5
จงออกแบบอัลกอริทึมที่เมื่อรับ directed graph มาหนึ่งกราฟแล้ว คำนวณหา cycle ใน มาหนึ่งวง วงใดก็ได้ ถ้าไม่มี cycle ก็ให้ตอบว่าไม่มี อัลกอริืทึมของคุณควรจะทำงานได้ในเวลา
ข้อ 6
ถ้า เป็น directed graph และ ไม่มี cycle แล้ว เราเรียกว่า เป็น directed acyclic graph (DAG)
ข้อย่อย 6.1
จงพิสูจน์ว่าถ้าเรารัน DFSALL บน ที่เป็น DAG แล้ว สำหรับ edge ทุก edge เราจะได้ว่า เสมอ
ข้อย่อย 6.2
สำหรับ DAG หนึ่งๆ เราให้ topological ordering ของ คือการนำ vertex ต่างๆ ใน มาเรียงกัน โดยที่ถ้า ตามหลัง ใน topological ordering แล้วจะไม่มี path จาก ไปยัง
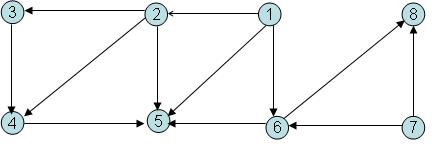
จากกราฟต่อไปนี้
จงหา topological ordering สักหนึ่ง ordering
ข้อย่อย 6.3
จงออกแบบอัลกอริทึมสำหรับหา topological ordering ของ DAG โดยใช้ DFSALL
ข้อย่อย 6.4
ใน directed graph เราเรียก vertex ว่าเป็น source ถ้าหากมี edge ใดๆ ชี้มายังมันเลย
จงพิสูจน์ว่าใน DAG จะมี source อยู่อย่างน้อยหนึ่ง vertex เสมอ
ข้อย่อย 6.5
จงออกแบบอัลกอริทึมสำหรับหา topological ordering ของ DAG โดยใช้ความจริงในข้อย่อย 6.4
ข้อ 7
[Dasgupta, Papadimitriou, Vazirani 3.18] คุณได้รับ tree (ในรูปแบบ adjacency list) รวมทั้ง root vertex
เรากล่าวคือ vertex เป็นบรรพบุรุษของ ถ้าหากว่ path จาก ไปยัง ต้องผ่าน
คุณต้องการทำการ precomputation ต้นไม้ที่ได้รับมาเพื่อหลังจากนั้นจะได้ตอบคำถามในรูปแบบที่ว่า "กำหนด vertex และ ในกราฟมาให้ จงหาว่า เป็นบรรพบุรุษของ หรือไม่?" ได้โดยใช้เวลา
จงออกแบบอัลกอริทึมเพื่อทำ precomputation ดังกล่าว รวมทั้งบอกวิธีตอบคำถามโดยใช้ข้อมูลที่ทำการคำนวณมาแล้ว อัลกอริืทึีมในการทำ precomputation ควรทำงานได้ในเวลา
ข้อ 8
[Dasgupta, Papadimitriou, Vazirani 3.19] คุณได้รับ tree (ในรูปแบบ adjacency list) รวมทั้ง root vertex นอกจากนี้ยังได้รับอะเรย์ของจำนวนเต็ม โดยที่ ถือเป็น "ค่า" ของ vertex
เราจะสร้างอะเรย์ ขึ้นมาใหม่โดยที่
- ค่า ที่มีค่ามากที่สุดสำหรับ vertex ทุก vertex ที่มี เป็นบรรพบุรุษ (รวมไปถึงตัว เองด้วย)
จงออกแบบอัลกอริทึมเพื่อคำนวนอะเรย์ ซึ่งทำงานได้ในเวลา











![{\displaystyle \mathrm {pre} [\cdot ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5f14bd567c1d4399b4eb7bf0cbec1384d6553f6)
![{\displaystyle \mathrm {post} [\cdot ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f54eb0703cdaaba891b1a544d81e7427ff8db727)
![{\displaystyle \mathrm {pre} [u]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57987c7ec8c947234dcbb4a4ba4716143db870b7)
![{\displaystyle \mathrm {post} [u]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/453354ce8d806d3623825e6778d83fb27a29a23c)
![{\displaystyle \mathrm {parent} [\cdot ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7f1c39f6e7ab57e4c484f1360a789a52ed88795)


![{\displaystyle \mathrm {pre} [u]<\mathrm {pre} [v]<\mathrm {post} [v]<\mathrm {post} [u]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0ff206bf4f368bf78732711c0de3d6e9fea6020)
![{\displaystyle \mathrm {pre} [v]<\mathrm {pre} [u]<\mathrm {post} [u]<\mathrm {post} [v]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37bd29f7c2f665b878a05288a07fe412124e2746)
![{\displaystyle [\mathrm {pre} [u],\mathrm {post} [u]]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8f747d4396f9e0518a50c30615449916d38bd29)
![{\displaystyle [\mathrm {pre} [v],\mathrm {post} [v]]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed6804f99f57a3e4c2241136a53c3bb2e191f7e)

![{\displaystyle \mathrm {pre} [v]<\mathrm {pre} [u]<\mathrm {post} [u]<\mathrm {pre} [v]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/127fa5c4d2b4a9d35b7819b40abbaa581e8f6cf9)

![{\displaystyle \mathrm {post} [u]>\mathrm {post} [v]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d599ab5a331b2c373a1f892e84467c6e5aa8dfbc)





![{\displaystyle x[\cdot ]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c884539a083374f7d563caab7d021bb134c2f3d)
![{\displaystyle x[u]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90a7a5651765638904d0897b85b8738cac0ab08f)
![{\displaystyle z[\cdot ]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75d25bed439a5462b7c11b7a2113ee96bf03dc02)
![{\displaystyle z[u]=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f98f09a1c1211237fdbbda7d3ff12fb22344d238)
![{\displaystyle x[v]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a6f21e91218494690fa84c4c1dc31cb31fa9a2e)