204512/บรรยาย 5

ทบทวน

Graph

เซตของโหนด $V$
เซตของเส้นเชื่อม $E\subseteq VxV$
ตัวอย่าง

จะกล่าวว่าเส้นเชื่อม (u,v) ติดกับโหนด u และ v

u และ v เป็นจุดปลายของเส้นเชื่อม (u,v)

degree ของโหนดใดๆ คือ จำนวนเส้นเชื่อมที่ติดกับโหนดนี้

path คือ ลำดับของโหนด $V_{1},V_{2},....,V_{k}$ ที่

$(V_{i},V_{i+1})\in E$ สำหรับทุกๆ $1\leq i\leq k$ เรียก $V_{1}$ เป็นจุดเริ่มต้น ,$V_{k}$ เป็นจุดสิ้นสุด

Thm

ถ้ากราฟ $G=(V,E)$ มี m edge ให้ deg(u) แทน degree ของโหนด u

$\sum _{u\in v}deg(u)=2m$

Def

กราฟ G Connected ถ้าทุกๆ โหนด u มี path ไปยังทุกๆ โหนด v

$C\subseteq V$เป็น connected coponent ใน G ตัว ทุกๆ โหนดใน C มี path ไปถึงทุกๆ โหนดใน C และ
ไม่มี path ไปยังโหนด v อื่นๆ ที่ $V\in V-C$
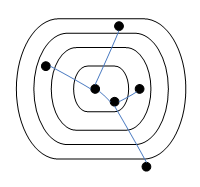
Cycle คือ path ที่มีจุดเริ่มต้นเป็นจุดเดียวกับจุดสิ้นสุด ดังรูป

Def. tree คือ กราฟที่ Connected และไม่มี Cycle
Thm. ข้อความข้างล่างนี้ให้ G มี n node

1) G Connected

2) G ไม่มี Cycle

3) G มีเส้นเชื่อม n-1 เส้น

2 ข้อใดๆ จะ imply ข้อที่ 3 และ imply ว่า G เป็น tree

Proof (1,2-->3)

(I) ถ้า G Connected,G จะต้องมีอย่างน้อย n-1 edge

(II) ถ้า G มี $\geq n$ edge G มี Cycle

เพราะฉะนั้น G ไม่มี Cycle , G มี $1\leq n-1$ edge

---

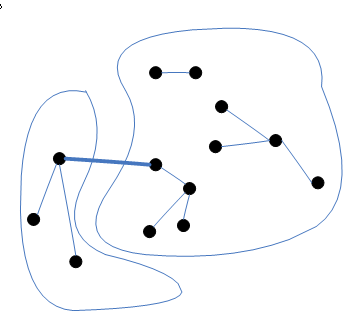
Spanning tree

ให้กราฟ G = (V,E) เรียก tree ว่าเป็น spanning tree ถ้า $E'\subseteq E$

---

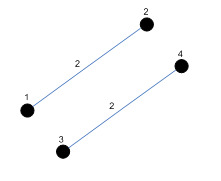
ปัญหา minimum spanning tree

ให้กราฟ G = (V,E) พร้อมด้วยฟังก์ชั่นน้ำหนัก w บนเส้นเชื่อม ต้องการหา spanning tree

T ที่ผลรวมของ weight บนเส้นเชื่อมน้อยที่สุด

---

Greedy framework

ทุกๆ เส้นเชื่อมจะมี

• ไม่มีสี(unknow)
• สีน้ำเงิน(accept)
• สีแดง(reject)

---

Invariant

จะมี minimum spanning tree ที่มีเส้นเชื่อมสีน้ำเงินทั้งหมดและไม่มีเส้นเชื่อมสีแดง

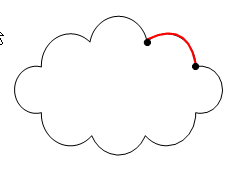
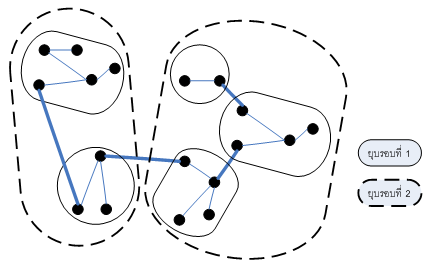
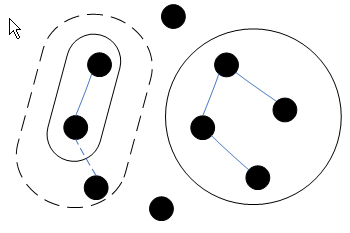
cut คือ partition ของเซตของโหนดออกเป็นสองส่วน$(X,{\overline {X}})$

เส้นเชื่อม e ข้าม Cut $(X,{\overline {X}})$ ถ้าจุดปลายด้านหนึ่งของ edge อยู่ใน X อีกช่วงอยู่ใน ${\overline {X}}$

---

Blue Rule และ Red Rule

blue rule พิจารณา Cut ใดๆ ที่ไม่มีเส้นเชื่อมสีน้ำเงินข้าม cut นั้น เลือกเส้นเชื่อมที่มีน้ำหนักน้อยสุด และให้ e มีสีน้ำเงิน

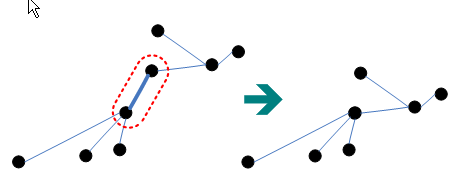
red rule พิจารณา Cycle ใดๆ ที่ไม่มี edge สีแดงอยู่เลือกเส้น e ที่น้ำหนักมากสุดให้ e มีสีแดง

ตัวอย่าง

Thm.

สามารถทำตาม blue rule/red rule ได้จนกระทั่งทุกๆ edge มีสีและตลอดการทำงาน invariant เป็นจริง

Proof

เมื่อเริ่มต้น (ทุกๆ edge ไม่มีสี)ทุกๆ เส้นเชื่อมไม่มีสี invariant เป็นจริง

assume ว่า invariant จริงมี minimum spanning tree ตาม invariant

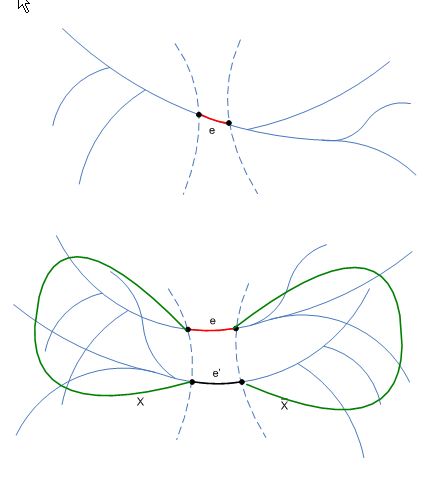
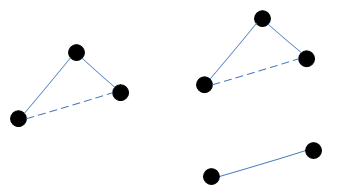
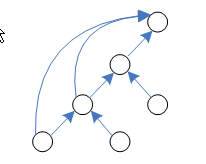
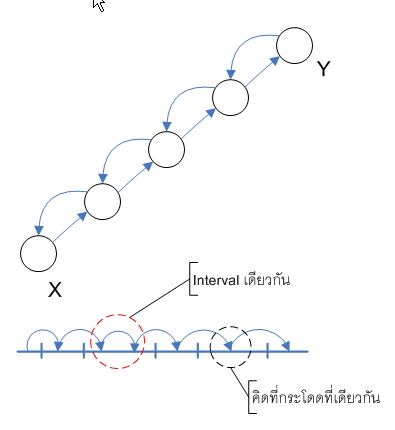
blue rule ถ้า apply blue rule กับ edge e,บน cut$(X,{\overline {X}})$ ถ้า $e\in T$ assume ว่า $e\notin T$ ดังรูป

เนื่องจาก T เป็น Spanning tree มี path จาก u ไป v บน T

path นี้จะต้องข้าม $(X,{\overline {X}})$ จะมี $e'\in T$ ที่ข้าม cut $(X,{\overline {X}})$
Claim

---

Blue Forest

---

Buruvka

---

Prim's Algorithm

---

Kruskal's Alogorithm

---

Path Compress

---