204512/บรรยาย 9

Dynamic Programming

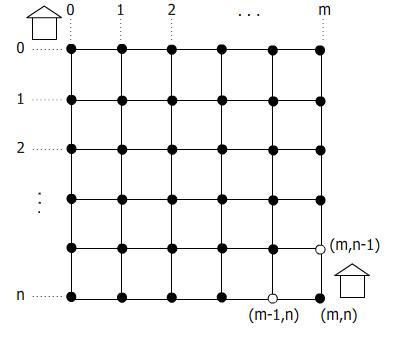
สมมุติต้องการเดินทางจากบ้าน ดช. ก ไปบ้าน ดญ. ข ระหว่างบ้าน ดช. ก กะ ดญ. ข ก็มีถนนตัดกันไปเรื่อยๆ คำถามคือ จากบ้าน ดช. ก ไปยังบ้าน ดญ.ข สามารถเดินทางโดยใช้เส้นทางต่างกันได้กี่แบบ

คำตอบคือ สามารถเลือกได้ ${\begin{pmatrix}n+m\\m\end{pmatrix}}$ แบบ หรือ ${\begin{pmatrix}n+m\\n\end{pmatrix}}$ แบบ

C(m,n) = C(m-1, n) + C(m,n-1)

C(0,0) เลือกได้ 1 วิธี

C(x,y) = 0 ถ้า x<0 หรือ y<0

ในกรณีที่มีการ block เส้นทาง เราอาจจะเขียน pseudo code ได้ ให้ recursive ไปที่จุดที่ col-1, row-1 ไปเรื่อยๆ

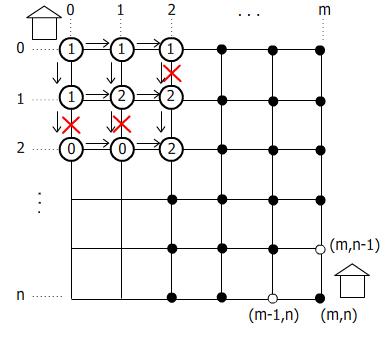
วิธีหนึ่งที่ใช้หาเส้นทาง

วิธีนี้เราจะทำการมองไปที่ทุกจุด โดยค่าที่แต่ละจุดเกิดจากผลรวมน้ำหนักของโหนดก่อนหน้า ดังนั้นวิธีนี้ใช้เวลาเป็น O(mn)

Dynamic programming คือการคำนวนมาก่อนเพื่อหาผลเฉลย

Example

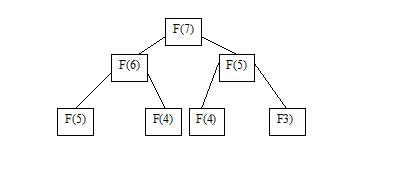
Function revolenchy

F(0) = F(1) = 1

F(1) = F(i-1) + F(i-2) เมื่อ i>1

สังเกตว่ามันมีกรณีซ้ำซ้อนเกิดขึ้น

F[0]<-F[1]<=1

For i=2 to n do
F[i]<-F[i-1] + F[i-2]
Return F[n]

นั่นคือ ถ้าอยากรู้ f(i) ต้องรู้ f(i-1), f(i-2)

---

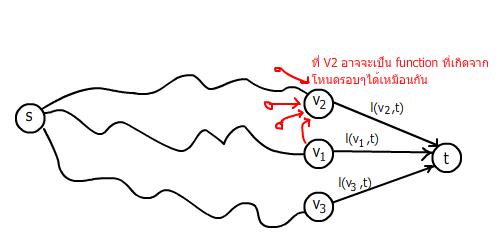
Shortest path บน DAG (Directed Acyclic Graph)

เราหา shortest path อย่างไร จาก st

t อาจมีตัวติดกันมากมาย shortest path ที่มาจาก ts ได้ ถ้ามีนผ่าน $v_{1}$, $v_{2}$, $v_{3}$ พวกนี้ต้องเป็น shortest path ด้วยเช่นเดียวกัน

ถ้ามองแบบ recursive เราจะค่อยคลี่ออกแล้วมองปัญหาย่อยๆ

$f(n)=min{\begin{cases}D(v1)+l(v1,t)\\D(v2)+l(v2,t)\\D(v3)+l(v3,t)\end{cases}}$

เราสามารถหาโดยไม่ต้องทำ recursive ก็ได้ โดยเรา evaluate ไปในทิศทางที่ขึ้นต่อกันเรื่อยๆ evaluate ด้วยลำดับที่เราเรียกว่า tropical order ถ้าเรียงลำดับตาม tolopical order (คือเป็น order ที่ edge ชี้จากโหนดน้อย->มาก)
S = $v_{0}$, $v_{1}$, $v_{2}$, $v_{3}$, … , $v_{n}$
Foreach vi, D(v1) <- infinity
D(v0) <- 0
For I = 1,…,n:
D(vi) = min [D(Vj) + l(vj,vi)]

                     Vj: (Vj, Vi) E E

ขั้นตอนการแก้ปัญหา dynamic programming
1. เขียน recurrence (เริ่มต้นนิยามปัญหาย่อย)
2. หาลำดับเพื่อ evaluate
3. เขียน pseudo code

Example

ถ้าเรามีเหรียญ 3, 5 บาท เราจะประกอบเหรียญให้เป็นเงินจำนวนไม่เกิน 100 บาท ได้กี่วิธี (ใช้เหรียญกี่เหรียญก็ได้)

เราอาจจะ plot เป็นตารางดังนี้

ตารางนี้เราทำการเก็บว่า ค่าไหนที่เกิดจากผลรวมของตัวมันบ้าง ซึ่งอาจจะให้ผลดีขึ้นถ้าเราเก็บด้วยว่าเราใช้เหรียญไปกี่เหรียญ

Example P(i) แทนจำนวนเหรียญที่เราใช้แล้วรวมกันได้ i บาท

$P(i)=min{\begin{cases}P(i-1)+1\\P(i-3)+1,&{\mbox{if }}i-3>=0\\P(i-4)+1,&{\mbox{if }}i-4>=0\end{cases}}$

ตัวอย่างนี้เราสามารถหาเหรียญที่ใช้น้อยที่สุดได้

ถ้าถามต่ออีกว่า เราจะรู้ได้หรือไม่ ว่าใช้เหรียญอะไรไปบ้าง? วิธีการคือ เราจะเก็บ pointer ไว้ เพื่อดูว่าค่าผลรวมได้มาจากการรวมเหรียญไหนไปบ้าง </math>

Example

มีถุงความจุเป็น L หน่วย
มีสินค้า k ประเภท
ประเภทที่ i, มีน้ำหนัก wi หน่วย
มีมูลค่า vi หน่วย

ให้หาสินค้าใส่ถุงโดย
1. ความจุรวม = L
2. มูลค่ารวมมากที่สุด

เลือกสินค้าที่ i มา 1 ชิ้น จะได้ว่า
1. P(i) = max P(i-wj) + Vj j:wj <= i 2. คำตอบคือ max P(i)

                 i: i <= L

A(i) = arg min P(i-wj) + Vj

อัลกอริทึมนี้ จะรันอยู่ในเวลา O(kL)
คำตอบนี้สำหรับปัญหาที่มี จำนวนสินค้าได้ไม่อั้น
แต่สำหรับสินค้าที่มี จำนวนกัด เราจะแก้ไขปัญหาได้อย่างไร
ปัญหาลักษณะนี้เราเรียกว่า Knapsack problem

Knapstack

ถุงมีความจุ L หน่วย
มีของ k ชิ้น
ชิ้นที่ i หนัก $w_{i}$, มีมูลค่า $v_{L}$

ต้องการหาเซตของ ของ ที่
(1) น้ำหนักรวมของ ของ รวมไม่เกิน L
(2) มีมูลค่ารวมมากที่สุด

• ต้องจัดลำดัับการหยิบให้ดี เพราะ ของแต่ละแบบมีชิ้นเดียว
  

hint: มีตัวแปร 2 ตัว

sol
จัดการหยิบของให้มีลำดับ

        เอาของชิ้นที่ 1 -> หยิบ
                   -> ไม่่หยิบ
        เอาของชิ้นที่ 2 -> หยิบ
                   -> ไม่่หยิบ
        เอาของชิ้นที่ 3 -> หยิบ
                   -> ไม่่หยิบ
                 .
                 .
                 .
        เอาของชิ้นที่ n -> หยิบ
                   -> ไม่่หยิบ

ให้
$A(i,j)$ แทนมูลค่ามากที่สุดที่ทำได้เมื่อน้ำหนักรวม = i และใช้ของไม่เกินชิ้นที่ j
$A(i,j)=max{\begin{cases}A(i,j-1)\\v_{j}+A(i-w_{j},j-1),&{\mbox{if }}i>=w_{j}\end{cases}}$

ตาราง L??????

ชิ้นที่	น้ำหนัก	มูลค่า
1	7	8
2	4	5
3	4	5
4	2	3
5	1	1

ตัวอย่าง : Longest Common Substring ให้ string S, T
ต้องการหา substring U ที่มีความยาวมากที่สุดที่เป็นทั้ง substring ของ S และ T
sol
string A เป็น substring ของ B
ถ้าเราสามารถสร้าง A ได้โดยการลบตัวอักษรบางตัวจาก B (หรือไม่ลบก็ได้)

ให้ n = |S| , m = |T|
S = AAGGATTCCAAGGAAAAGTTAG
T = GGTCCAGCCCAGCCATTGCAGTT

สำหรับ string S ใดๆ
ให้ $S_{i}$ แทน prefix ความยาว i ของ S
ex
$S_{5}$ = AAGGA
T = GGT
หา longest common substring ของ $S_{n}$ กับ $T_{m}$

L(i,j) = ความยาวของ longest common substring ของ $S_{i}$ กับ $T_{i}$
รูป?????
$L(i,j)=max{\begin{cases}L(i,j-1)\\L(i-1,j)\\L(i-1,j-1)+1,&{\mbox{if }}S[i]=T[j]\\L(i-1,j-1),&{\mbox{if }}S[i]!=T[j](optionalcase)\end{cases}}$

ทดลอง fill ตาราง
ตาราง????
ใช้เวลา O(mn)

Optimal Binary Search Tree

Data	1	2	3	4	5	6	7
Acess	3	2000	4	2	10	5	10000