ผลต่างระหว่างรุ่นของ "418531 ภาคต้น 2552/โจทย์ปัญหาการวิเคราะห์เชิงเส้นกำกับ/เฉลยข้อ 3"
ไปยังการนำทาง
ไปยังการค้นหา
Aoy (คุย | มีส่วนร่วม) |
Aoy (คุย | มีส่วนร่วม) |
||
| (ไม่แสดง 12 รุ่นระหว่างกลางโดยผู้ใช้คนเดียวกัน) | |||
| แถว 4: | แถว 4: | ||
จากโจทย์ <math>a=2, b =2, f(n) = n^3 </math> | จากโจทย์ <math>a=2, b =2, f(n) = n^3 </math> | ||
| − | จะได้ <math>n^{log_b a}=n^{log_2 2}=n</math> | + | จะได้ <math>n^{\log_b a}=n^{\log_2 2}=n</math> |
จะได้ <math>a(f((n/b))=2f(n/2)=(1/4)n^3 \leq n^3</math> เมื่อ <math>c = 1/4</math> | จะได้ <math>a(f((n/b))=2f(n/2)=(1/4)n^3 \leq n^3</math> เมื่อ <math>c = 1/4</math> | ||
| แถว 15: | แถว 15: | ||
จะได้ <math>a=1, b= 10/9, f(n) = n</math> | จะได้ <math>a=1, b= 10/9, f(n) = n</math> | ||
| − | หา <math>n^{log_b a}=n^{log_{10/9} 1=n^0=1}</math> | + | หา <math>n^{\log_b a}=n^{\log_{10/9} 1=n^0=1}</math> |
หา <math>a(f(n/b))=f(9n/10)=9n/10 \leq n</math> เมื่อ <math>c = 9/10</math> | หา <math>a(f(n/b))=f(9n/10)=9n/10 \leq n</math> เมื่อ <math>c = 9/10</math> | ||
| แถว 26: | แถว 26: | ||
จะได้ <math>a=16, b= 4, f(n) = n^2</math> | จะได้ <math>a=16, b= 4, f(n) = n^2</math> | ||
| − | หา <math>n^{log_b a}=n^{log_4 16}=n^2</math> | + | หา <math>n^{\log_b a}=n^{\log_4 16}=n^2</math> |
| − | ดังนั้น <math>T(n) = \Theta(n^{log_b a} \lg n) = \Theta(n^2 \lg n)</math> | + | ดังนั้น <math>T(n) = \Theta(n^{\log_b a} \lg n) = \Theta(n^2 \lg n)</math> |
== ข้อย่อย 4 == | == ข้อย่อย 4 == | ||
| − | + | ใช้ master method กรณีที่ 3 | |
| + | |||
| + | จะได้ <math>a=7, b= 3, f(n) = n^2</math> | ||
| + | |||
| + | หา <math>n^{\log_b a}=n^{\log_3 7}</math> | ||
| + | |||
| + | หา <math>a(f(n/b))=7(f(n/3))=(7/9)n^2 \leq n^2</math> เมื่อ <math>c = 7/9</math> | ||
| + | |||
| + | ดังนั้น <math>T(n) = \Theta(f(n)) = \Theta(n^2)</math> | ||
| + | |||
| + | == ข้อย่อย 5 == | ||
| + | ใช้ master method กรณีที่ 1 | ||
| + | |||
| + | จะได้ <math>a=7, b= 2, f(n) = n^2</math> | ||
| + | |||
| + | หา <math>n^{\log_b a}=n^{\log_2 7}</math> | ||
| + | |||
| + | ดังนั้น <math>T(n) = \Theta(n^{\log_b a})= \Theta(n^{\log_2 7})</math> | ||
== ข้อย่อย 6 == | == ข้อย่อย 6 == | ||
| − | + | ใช้ master method กรณีที่ 2 | |
| + | |||
| + | จากโจทย์ <math>a=2, b =4, f(n) = n^{1/2} </math> | ||
| + | |||
| + | จะได้ <math>n^{\log_b a}=n^{\log_4 2}=n^{1/2}</math> | ||
| + | |||
| + | |||
| + | ดังนั้นจะได้ว่า <math>T(n)= \Theta (n^{\log_b a} \lg n) = \Theta(\sqrt{n} \lg n) </math> | ||
== ข้อย่อย 7 == | == ข้อย่อย 7 == | ||
| − | + | ||
| + | [[ไฟล์:7.JPG]] | ||
| + | |||
| + | == ข้อย่อย 8 == | ||
| + | |||
| + | [[ไฟล์:8.JPG]] | ||
| + | |||
| + | == ข้อย่อย 9 == | ||
| + | ใช้ master method กรณีที่ 1 | ||
| + | |||
| + | จากโจทย์ <math>a=3, b =2, f(n) = n \log n </math> | ||
| + | |||
| + | จะได้ <math>n^{\log_b a}=n^{\log_2 3}</math> | ||
| + | |||
| + | ดังนั้นจะได้ว่า <math>T(n)= \Theta (n^{\log_b a}) = \Theta(n^{\log_2 3}) </math> | ||
รุ่นแก้ไขปัจจุบันเมื่อ 08:14, 5 สิงหาคม 2552
เนื้อหา
ข้อย่อย 1
ใช้ master method กรณีที่ 3
จากโจทย์
จะได้
จะได้ เมื่อ
ดังนั้นจะได้ว่า
ข้อย่อย 2
ใช้ master method กรณีที่ 3
จะได้
หา
หา เมื่อ
ดังนั้น
ข้อย่อย 3
ใช้ master method กรณีที่ 2
จะได้
หา
ดังนั้น
ข้อย่อย 4
ใช้ master method กรณีที่ 3
จะได้
หา
หา เมื่อ
ดังนั้น
ข้อย่อย 5
ใช้ master method กรณีที่ 1
จะได้
หา
ดังนั้น
ข้อย่อย 6
ใช้ master method กรณีที่ 2
จากโจทย์
จะได้
ดังนั้นจะได้ว่า
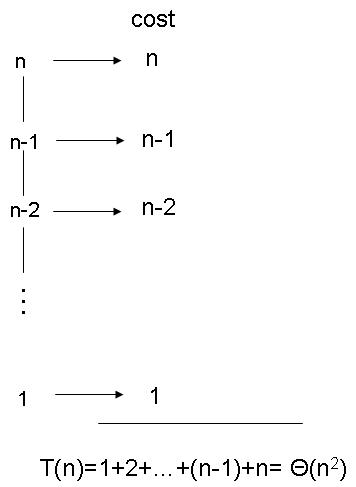
ข้อย่อย 7
ข้อย่อย 8
ข้อย่อย 9
ใช้ master method กรณีที่ 1
จากโจทย์
จะได้
ดังนั้นจะได้ว่า