418341 ภาคต้น 2552/โจทย์ปัญหาอัลกอริืทึมเกี่ยวกับกราฟ

ข้อ 1

ในชั้นเรียนเราได้พูดถึงการเก็บ undirected graph ด้วย adjacency matrix และ adjacency list

ถ้าเราจะเก็บ directed graph ด้วย adjacency matrix และ adjacency list บ้าง จะต้องเปลี่ยนแปลงรูปแบบการจัดเ็ก็บอย่างไรบ้าง?

ข้อ 2

[Dasgupta, Papadimitriou, Varizari 3.5] กำหนดกราฟแบบมีทิศทาง $G=(V,E)\,$ มาให้ กราฟผันกลับ (reverse) ของ $G\,$ คือกราฟ $G^{R}=(V,E^{R})\,$ โดยที่มีเซตของ vertex เป็นเซตเดียวกันแต่ edge ใน $G^{R}\,$ คือ edge ใน $G\,$ ที่ถูกกลับข้าง (กล่าวคือ $E^{R}=\{(v,u)\ |\ (u,v)\in E\}\,$)

จงออกแบบอัลกอริทึมที่เมื่อให้ $G\,$ ในรูปแบบ adjacency list ให้คำนวณ $G^{R}\,$ ในรูปแบบ adjacency เช่นกัน อัลกอริทึมของคุณควรจะทำงานได้ในเวลา $O(|V|+|E|)\,$

ข้อ 3

1. [Kleinberg & Tardos 3.2] จงออกแบบอัลกอริืทึมที่ตรวจสอบว่า undirected garph $G\,$ ที่ให้มาในรูปแบบ adjacency list มี cycle หรือไม่ ถ้ามีให้พิมพ์ออกมาหนึ่ง cycle (วงไหนก็ได้) อัลกอริึทึมของคุณควรจะทำงานได้ในเวลา $O(n+m)\,$ เมื่อ $n\,$ คือจำนวน vertex $m\,$ คือจำนวน edge
2. [Dasgupta, Papadimitriou, Vazirani 3.11] จงออกแบบอัลกอริทึมที่ เมื่อให้ directed graph $G=(V,E)\,$ และให้ edge $e\in E\,$ มา แล้วคำนวณว่ามี cycle ที่มี $e\,$ เป็น edge หนึ่งอยู่ีใน cycle นั้นหรือไม่ ถ้ามีให้พิมพ์ออกมาสักหนึ่ง cycle อัลกอริทึมของคุณควรจะทำงานได้ในเวลา $O(n+m)\,$

ข้อ 4

สมมติว่าเราอัลกอริทึมในการทำ depth first search ให้สร้างอะเรย์ขนาด $n\,$ ช่อง เมื่อ $n\,$ คือจำนวน vertex เพิ่มขึ้นอีกสองอะเรย์ ได้แก่ $\mathrm {pre} [\cdot ]$ และ $\mathrm {post} [\cdot ]$ โดยมีตัวแปร global ชื่อ clock ซึ่งมีค่าเริ่มแรกเท่ากับ 1 เป็นตัวช่วย ดังต่อไปนี้

<geshi lang="c"> DFS(u) {

   pre[u] = clock
   clock = clock + 1
   explored[u] = 1
   
   for i = 1 to d[u] do
   {
       v = a[u][i]
       if explored[v] = 0 then
       {
           parent[v] = u
           DFS(v)
       }
   }

   post[u] = clock
   clock = clock + 1

} </geshi>

กล่าวคือ $\mathrm {pre} [u]\,$ เป็นเหมือนเวลาที่ DFS(u) เริ่มทำงาน และ $\mathrm {post} [u]\,$ เป็นเวลาที่ DFS(u) ทำงานเสร็จ

นอกจากนี้ในการทำ depth first search เราจะพยายามเรียก DFS(u) ที่ทุก vertex u ในกราฟหามันยังไม่เคยถูกไปถึงด้วย DFS มาก่อน ดังต่อไปนี้

<geshi lang="c"> DFSALL() {

    for u = 1 to n do
         if explored[u] = 0 then
         {
              parent[u] = 0
              DFS(u)
         }

} </geshi>

ข้อย่อย 4.1

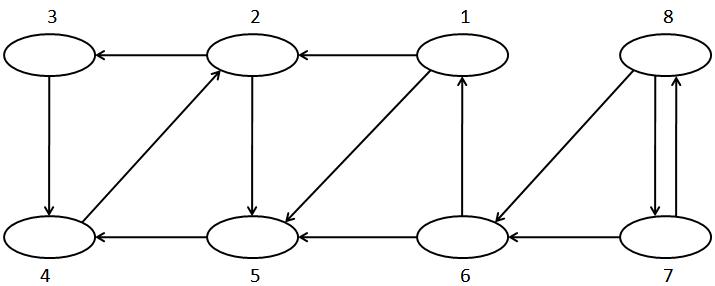
พิจารณากราฟแบบมีทิศทางข้างล่างนี้

จงรัน DFSALL บนกราฟข้างบน โดยเวลาไล่ vertex ให้ไล่จาก vertex ที่มีหมายเลขน้อยไปยังมากหมายเลขมาก (ยกตัวอย่างเช่น vertex ที่มี edge พุ่งออกจาก 7 ไปถึง ได้แก่ vertex 6 และ 8 เป็นต้น) แล้วเขียน

1. DFS tree
2. อะเรย์ $\mathrm {parent} [\cdot ]$
3. อะเรย์ $\mathrm {pre} [\cdot ]$
4. อะเรย์ $\mathrm {post} [\cdot ]$

ข้อย่อย 4.2

หากเราจำแนก edge ในกราฟข้างบนออกเป็น 4 ประเภท ตังต่อไปนี้

• Tree edge คือ edge ที่อยู่บน DFS tree ที่ได้จากการทำ DFS
• Back edge คือ edge ที่พุ่งออกจาก vertex ไปหาบรรพบุรุษของมันใน DFS tree
• Forward edge คือ edge ที่พุ่งออกจาก vertex ไปหาลูกหลานของมันใน DFS tree
• Cross edge คือ edge อื่นๆ ที่ไม่เข้าพวกทั้งสามข้างต้น

แล้วจงบอกว่า edge ในกราฟเป็น edge แต่ละ edge เป็น edge ชนิดใดบ้าง

ข้อย่อย 4.3

ให้ $G=(V,E)\,$ เป็นกราฟแบบมีทิศทาง สมมติว่าเรารัน DFSALL บน $G\,$ แล้ว จงพิสูจน์ "สมบัติวงเล็บ" ต่อไปนี้:

ถ้า $u\,$ และ $v\,$ เป็น vertex สอง vertex ใดๆ ในกราฟแล้ว ภายในข้อเท็จจริงสามข้อต่อไปนี้ จะมีข้อเท็จจริงข้อหนึ่งเป็นจริง และมันจะเป็นจริงเพียงข้อเดียวเท่านั้น

1. $\mathrm {pre} [u]<\mathrm {pre} [v]<\mathrm {post} [v]<\mathrm {post} [u]\,$
2. $\mathrm {pre} [v]<\mathrm {pre} [u]<\mathrm {post} [u]<\mathrm {post} [v]\,$
3. ช่วง $[\mathrm {pre} [u],\mathrm {post} [u]]\,$ และช่วง $[\mathrm {pre} [v],\mathrm {post} [v]]\,$ ไม่มีสมาชิกร่วมกันเลย

ข้อย่อย 4.4

จงพิสูจน์ว่า สำหรับ edge $e=(u,v)\,$ ใดๆ เราสามารถใช้สมบัติวงเล็บข้างต้นในการจำแนกประเภทของมันได้

• ถ้า $\mathrm {pre} [u]<\mathrm {pre} [v]<\mathrm {post} [v]<\mathrm {post} [u]\,$ แล้ว $e\,$ ต้องเป็น tree edge หรือ forward edge
• ถ้า $\mathrm {pre} [v]<\mathrm {pre} [u]<\mathrm {post} [u]<\mathrm {pre} [v]\,$ แล้ว $e\,$ ต้องเป็น back edge
• ถ้า $[\mathrm {pre} [u],\mathrm {post} [u]]\,$ และ $[\mathrm {pre} [v],\mathrm {post} [v]]\,$ ไม่มีส่วนร่วมกัน แล้ว $e\,$ ต้องเป็น cross edge