ผลต่างระหว่างรุ่นของ "418531 ภาคต้น 2552/โจทยปัญหาอัลกอริทึมแบบแบ่งแยกแล้วเอาชนะ/เฉลยข้อ 3"

รุ่นแก้ไขปัจจุบันเมื่อ 07:48, 4 กันยายน 2552

อินพุต: อะเรย์ที่เรียงแล้วจำนวน k อะเรย์ แต่ละอะเรย์มีสมาชิกอยู่ $n\,$ ตัว

เอาพุต: รวมอะเรย์ที่เป็นอินพุตให้เป็นอะเรย์ที่เรียงแล้วขนาด $kn\,$ ช่อง

วัตถุที่เราต้องตรวจสอบคือ สมาชิกแต่ละตัวในแต่ละอะเรย์ เงื่อนไขคือ อะเรย์สุดท้ายที่ใช้รวมต้องเรียงด้วย

ข้อย่อย 1

พิจารณาการรวมอะเรย์ดังต่อไปนี้

ขั้นตอนที่ 1 การรวมอะเรย์ที่เรียงแล้วขนาด

n\,

ตัวที่หนึ่ง เข้ากับอะเรย์ที่เรียงแล้วขนาด

n\,

ตัวที่สอง เวลาในการรวมจะเป็น

2n\,

ขั้นตอนที่ 2 การรวมอะเรย์ที่เรียงแล้วขนาด

2n\,

จากขั้นตอนที่ 1 เข้ากับอะเรย์ที่เรียงแล้วขนาด

n\,

ตัวที่สาม เวลาในการรวมจะเป็น

3n\,

ขั้นตอนที่ k-1 การรวมอะเรย์ที่เรียงแล้วขนาด

(k-1)n\,

จากขั้นตอนที่ k-2 เข้ากับอะเรย์ที่เรียงแล้วขนาด

n\,

ตัวที่ k เวลาในการรวมจะเป็น

kn\,

ดังนั้นเวลารวมทั้งหมดจะเป็น

2n+3n+...+kn=O(nk^{2})\,

ข้อย่อย 2

แนวคิด จะทำคล้าย ๆ กับ merge sort ธรรมดา โดยการรวมจะรวมอะเรย์สองตัวที่มีขนาด $n\,$ เข้าด้วยกันให้เป็นอะเรย์ที่มีขนาด $2n\,$ หลังจากนั้น รวมอะเรย์ที่มีขนาด $2n\,$ เข้าเป็นอะเรย์ที่มีขนาด $4n\,$ ทำแบบนี้ไปเรื่อย ๆ จนได้อะเรย์ที่เรียงแล้ว และมีขนาดเป็น $kn\,$

ส่วนเวลาการทำงาน สามารถคิดได้ดังนี้ ในการรวมอะเรย์ที่มีขนาด $n\,$ เข้าด้วยกันให้เป็นอะเรย์ที่มีขนาด $2n\,$ นั้น แต่ละคู่จะใช้เวลา $2n=O(n)\,$ ซึ่งมีทั้งหมด $k/2\,$ คู่ ดังนั้นเวลาการทำงานทั้งหมดของ tree ชั้นนี้จะเป็น $(k/2)O(n)=O(kn)\,$ ส่วนชั้นที่สองที่เป็นการรวมอะเรย์ที่มีขนาด $2n\,$ เข้าเป็นอะเรย์ที่มีขนาด $4n\,$ นั้น แต่ละคู่จะใช้เวลา $4n=O(n)\,$ ซึ่งมีทั้งหมด $k/4\,$ คู่ ดังนั้นเวลาการทำงานทั้งหมดของ tree ชั้นนี้จะเป็น $(k/4)O(n)=O(kn)\,$ คิดแบบนี้ไปเรื่อย ๆ ก็จะได้เวลาการทำงานของแต่ละชั้นเป็น $O(nk)\,$ ซึ่ง tree มีทั้งหมด $\log k\,$ ชั้น ดังนั้นเวลาการทำงานทั้งหมด ก็จะเป็น $O(nk\log k)\,$

@@ แถว 5: / แถว 5: @@
 วัตถุที่เราต้องตรวจสอบคือ สมาชิกแต่ละตัวในแต่ละอะเรย์ เงื่อนไขคือ อะเรย์สุดท้ายที่ใช้รวมต้องเรียงด้วย
-== ข้อย่อย 1===
+== ข้อย่อย 1==
+พิจารณาการรวมอะเรย์ดังต่อไปนี้
+:ขั้นตอนที่ 1 การรวมอะเรย์ที่เรียงแล้วขนาด <math> n \, </math> ตัวที่หนึ่ง เข้ากับอะเรย์ที่เรียงแล้วขนาด<math> n \,</math> ตัวที่สอง เวลาในการรวมจะเป็น <math> 2n \,</math>
+:ขั้นตอนที่ 2 การรวมอะเรย์ที่เรียงแล้วขนาด <math> 2n \, </math> จากขั้นตอนที่ 1 เข้ากับอะเรย์ที่เรียงแล้วขนาด<math> n \,</math> ตัวที่สาม เวลาในการรวมจะเป็น <math> 3n \,</math>
+:ขั้นตอนที่ k-1 การรวมอะเรย์ที่เรียงแล้วขนาด <math> (k-1)n \, </math> จากขั้นตอนที่ k-2 เข้ากับอะเรย์ที่เรียงแล้วขนาด<math> n \,</math> ตัวที่ k เวลาในการรวมจะเป็น <math> kn \,</math>
+:ดังนั้นเวลารวมทั้งหมดจะเป็น <math> 2n+3n+...+kn=O(nk^2) \,</math>
-== ข้อย่อย 2===
+== ข้อย่อย 2 ==
+แนวคิด จะทำคล้าย ๆ กับ merge sort ธรรมดา โดยการรวมจะรวมอะเรย์สองตัวที่มีขนาด <math> n \, </math> เข้าด้วยกันให้เป็นอะเรย์ที่มีขนาด <math> 2n \, </math> หลังจากนั้น รวมอะเรย์ที่มีขนาด <math> 2n \, </math> เข้าเป็นอะเรย์ที่มีขนาด  <math> 4n \, </math> ทำแบบนี้ไปเรื่อย ๆ จนได้อะเรย์ที่เรียงแล้ว และมีขนาดเป็น <math> kn \, </math>
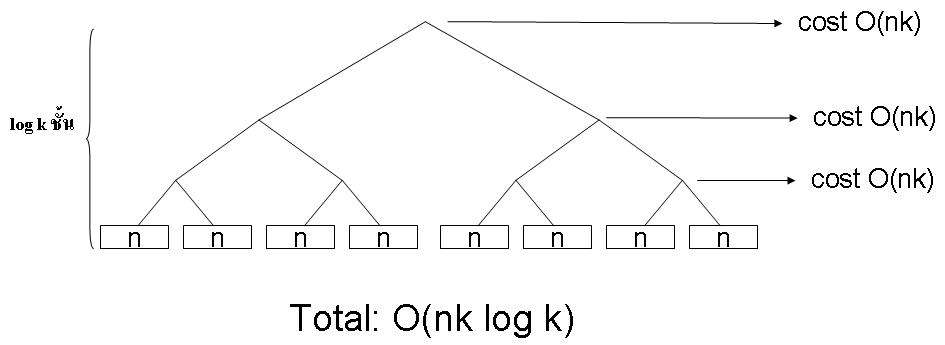
+ส่วนเวลาการทำงาน สามารถคิดได้ดังนี้ ในการรวมอะเรย์ที่มีขนาด <math> n \, </math> เข้าด้วยกันให้เป็นอะเรย์ที่มีขนาด <math> 2n \, </math> นั้น แต่ละคู่จะใช้เวลา <math> 2n=O(n) \,</math> ซึ่งมีทั้งหมด <math> k/2 \,</math> คู่ ดังนั้นเวลาการทำงานทั้งหมดของ tree ชั้นนี้จะเป็น <math> (k/2)O(n)=O(kn) \,</math> ส่วนชั้นที่สองที่เป็นการรวมอะเรย์ที่มีขนาด <math> 2n \, </math> เข้าเป็นอะเรย์ที่มีขนาด  <math> 4n \, </math> นั้น แต่ละคู่จะใช้เวลา <math> 4n=O(n) \,</math> ซึ่งมีทั้งหมด <math> k/4 \,</math> คู่ ดังนั้นเวลาการทำงานทั้งหมดของ tree ชั้นนี้จะเป็น <math> (k/4)O(n)=O(kn) \,</math> คิดแบบนี้ไปเรื่อย ๆ ก็จะได้เวลาการทำงานของแต่ละชั้นเป็น <math> O(nk) \,</math> ซึ่ง tree มีทั้งหมด <math> \log k \, </math> ชั้น ดังนั้นเวลาการทำงานทั้งหมด ก็จะเป็น <math> O(nk \log k) \,</math>
+[[ไฟล์:mergeLog.JPG]]

ผลต่างระหว่างรุ่นของ "418531 ภาคต้น 2552/โจทยปัญหาอัลกอริทึมแบบแบ่งแยกแล้วเอาชนะ/เฉลยข้อ 3"

รุ่นแก้ไขปัจจุบันเมื่อ 07:48, 4 กันยายน 2552

ข้อย่อย 1

ข้อย่อย 2

รายการเลือกการนำทาง

เครื่องมือส่วนตัว

เนมสเปซ

สิ่งที่แตกต่าง

ดู

เพิ่มเติม

ค้นหา

การนำทาง

เครื่องมือ