ผลต่างระหว่างรุ่นของ "204512-53/lecture11"
Nsmile (คุย | มีส่วนร่วม) |
|||
| แถว 90: | แถว 90: | ||
---- | ---- | ||
| + | Part II | ||
| + | |||
| + | [[ไฟล์:Np1.jpg]] | ||
รุ่นแก้ไขเมื่อ 09:04, 11 ตุลาคม 2553
จดบันทึกคำบรรยายโดย:
นายชัชพล นุโยค รหัส 5214550049 นายสุรเดช วัฒนอุดมโรจน์ รหัส 5214550324
part II
นายชัยณรงค์ เหมือนรุ่ง รหัสประจำตัว 5214550057 นายศศิน เทียนดี รหัสประจำตัว 5214550278 น.ส.นันทณัฏฐ์ ภูทอง รหัสประจำตัว 5214550171 น.ส.ชนาพร คุรุรัตน์พันธ์ รหัสประจำตัว 5214550031
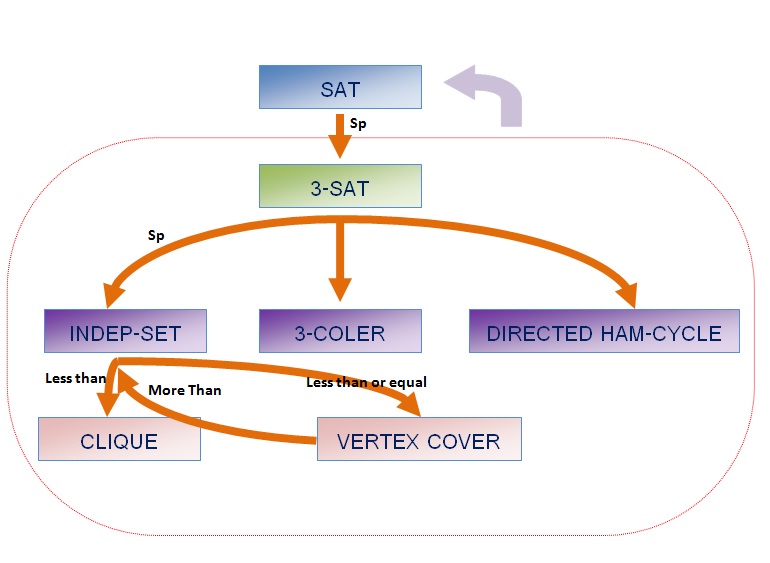
NP Completeness
NP: Non-deterministic Polynomial time คือ เซตของ Algorithm ที่ไม่สามารถแก้ไขปัญหาได้ในเวลาที่เป็น polynomial โดยการนิยามเซตของปัญหาเพื่อประโยชน์ในการเปรียบเทียบระดับความยาก-ง่ายของ Algorithm ซึ่งเซตของปัญหาสามารถแบ่งเป็นเซต P, NP, NP-hard และ NP-complete
ในการเปรียบเทียบ Algorithm ใดๆ เราจะทำการพิจารณา Algorithm ว่าจัดอยู่ในเซตของปัญหาใด โดยใช้เทคนิคการลดรูปของปัญหา (Reduction) ว่าเป็นกลุ่มเดียวกับปัญหาที่อยู่ในเซตหรือไม่ ถ้าอยู่ในกลุ่มเดียวกันจะกล่าวว่า Algorithm มีความยากเท่ากัน ความยาก คือ มี Algorithm ที่มีประสิทธิภาพแก้ไขปัญหาหรือไม่
ปัญหา A สัมพันธ์ ปัญหา B
ปัญหา A ไม่ยากไปกว่า ปัญหา B
โดยมีความหมายว่า ถ้ามี Algorithm ที่สามารถแก้ปัญหา B ได้ ปัญหา A ก็จะสามารถแก้ได้เช่นกัน
ปัญหาที่ 1 : Independent Set เป็นปัญหากลุ่ม Decision Problem
นิยาม : ให้ Undirected graph G = (V, E) จะกล่าวว่า I ![]() V เป็น Independent Set ก็ต่อเมื่อ สำหรับทุกๆโหนด
U,V
V เป็น Independent Set ก็ต่อเมื่อ สำหรับทุกๆโหนด
U,V ![]() I, U
I, U ![]() V ไม่มีเส้นเชื่อมระหว่าง U และ V
V ไม่มีเส้นเชื่อมระหว่าง U และ V
ปัญหา : ให้กราฟ G = (V, E) และ integer k, มี Independent set ขนาด ≥ k หรือไม่
ในภาพทำการเลือกโหนด (k) เท่ากับ 1 จะกล่าวว่ามี Independent set ขนาด 1
สามารถนำไปใช้แก้ปัญหา หาคนที่ไม่รู้จักกันในห้อง หรือ การเปิด-ปิดไฟแดงที่แยก
ปัญหาที่ 2 : Vertex Cover
นิยาม : C ![]() V เป็น Vertex Cover ก็ต่อเมื่อ
V เป็น Vertex Cover ก็ต่อเมื่อ ![]() (U,V)
(U,V)![]() E,U
E,U ![]() C หรือ V
C หรือ V ![]() C
C
ปัญหา : ให้กราฟ G = (V, E) และ จำนวนเต็ม k ถามว่ามี vertex cover ขนาด ≤ k หรือไม่
ถ้าสมมติให้ Independent Set ![]() Vertex Cover
Vertex Cover
Lemma : พิจารณาเซต A ![]() V ใดๆ ให้ A เป็น imdenpendent set โดย V-A เป็น Vertec Cover
V ใดๆ ให้ A เป็น imdenpendent set โดย V-A เป็น Vertec Cover
Proof : Indenpendent set ![]() Vertex Cover
Vertex Cover
นิยาม : ปัญหา A เป็น Polynomial time เพื่อลดปัญหา B ถ้ามี Algorithm T ที่ทำงานใน Polynomial time สำหรับทุกๆ instance X ของ A จะได้ T(x) เป็น instance ของ B
X' = T(x) เป็น instance ของ B และ |X'| = Poly (|X|)
ถ้า x เป็น instance ตอบ "Yes" ใน A => x' เป็น instance ตอบ "Yes" ใน B
ถ้า x เป็น instance ตอบ "No" ใน A => x' เป็น instance ตอบ "No" ใน B
Lemma : ถ้า A ![]() B และมี Algorithm ที่แก้ปัญหา B ได้ใน Polynomial time จะมี Algorithm ที่แก้ปัญหา A ใน Polynomial time ได้ด้วย
B และมี Algorithm ที่แก้ปัญหา B ได้ใน Polynomial time จะมี Algorithm ที่แก้ปัญหา A ใน Polynomial time ได้ด้วย
Proof : ให้ M เป็น Polynomial time Algorithm ที่แก้ปัญหา B
จะได้ว่า A ![]() B
นั้นคือ มี Polynomial time Algorithm T ที่
B
นั้นคือ มี Polynomial time Algorithm T ที่ ![]() instance x ของ A
x' = T(x) มีขนาด poly(|x|) และคำตอบของ x ในปัญหา A ตรงกับของ x' ในปัญหา B
instance x ของ A
x' = T(x) มีขนาด poly(|x|) และคำตอบของ x ในปัญหา A ตรงกับของ x' ในปัญหา B
สำหรับ Algorithm M' ดังนี้
M'(x) : x' = T(x) return M(x')
แต่เนื่องจาก |x'| = poly(|x|)
ดังนั้น เวลาในการคำนวณ M(x')คือ poly(|x'|) = poly(poly(|x|)) = poly(|x|)
จากนิยาม M'(x) เป็นคำตอบของ x ใน A เหลือแต่ต้องตรวจสอบว่า M' ทำงานใน Polynomial time หรือ poly(|x|)
Part II