ผลต่างระหว่างรุ่นของ "204512/บรรยาย 5"
ไปยังการนำทาง
ไปยังการค้นหา
Noonsri (คุย | มีส่วนร่วม) (→Graph) |
Noonsri (คุย | มีส่วนร่วม) (→Graph) |
||
| แถว 4: | แถว 4: | ||
เซตของโหนด <math>V</math><br> | เซตของโหนด <math>V</math><br> | ||
เซตของเส้นเชื่อม <math>E \subseteq VxV</math><br /> | เซตของเส้นเชื่อม <math>E \subseteq VxV</math><br /> | ||
| − | ตัวอย่าง <br> | + | '''ตัวอย่าง'''<br> |
[[ภาพ:MST1.png]]<br /> | [[ภาพ:MST1.png]]<br /> | ||
:จะกล่าวว่าเส้นเชื่อม (u,v) ติดกับโหนด u และ v<br> | :จะกล่าวว่าเส้นเชื่อม (u,v) ติดกับโหนด u และ v<br> | ||
รุ่นแก้ไขเมื่อ 02:21, 11 กรกฎาคม 2550
เนื้อหา
ทบทวน
Graph
เซตของโหนด
เซตของเส้นเชื่อม
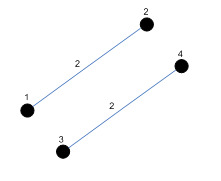
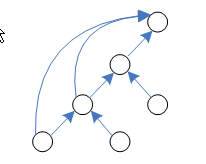
ตัวอย่าง

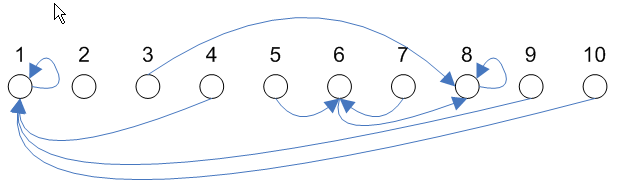
- จะกล่าวว่าเส้นเชื่อม (u,v) ติดกับโหนด u และ v
- u และ v เป็นจุดปลายของเส้นเชื่อม (u,v)
- degree ของโหนดใดๆ คือ จำนวนเส้นเชื่อมที่ติดกับโหนดนี้
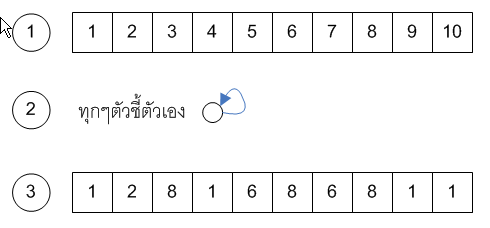
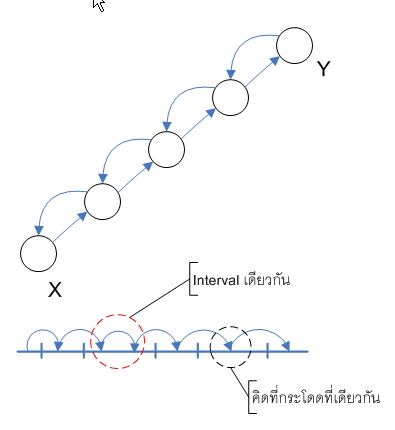
- path คือ ลำดับของโหนด ที่
- สำหรับทุกๆ เรียก เป็นจุดเริ่มต้น , เป็นจุดสิ้นสุด
Thm
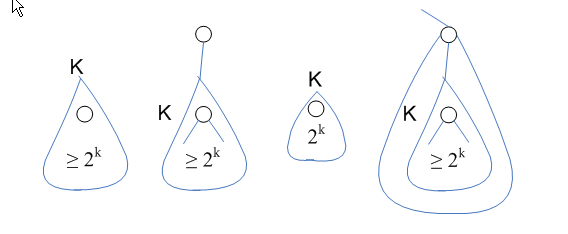
- ถ้ากราฟ มี m edge ให้ deg(u) แทน degree ของโหนด u
Def
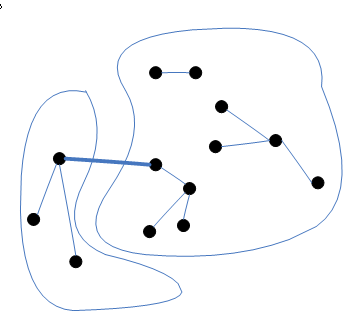
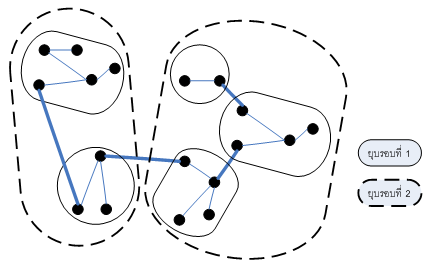
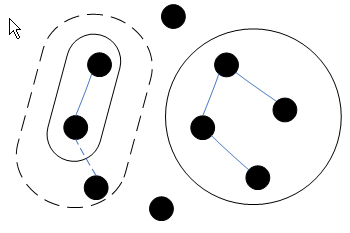
- กราฟ G Connected ถ้าทุกๆ โหนด u มี path ไปยังทุกๆ โหนด v
เป็น connected coponent ใน G ตัว ทุกๆ โหนดใน C มี path ไปถึงทุกๆ โหนดใน C และ
ไม่มี path ไปยังโหนด v อื่นๆ ที่
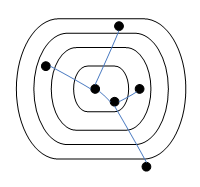
Cycle คือ path ที่มีจุดเริ่มต้นเป็นจุดเดียวกับจุดสิ้นสุด ดังรูป

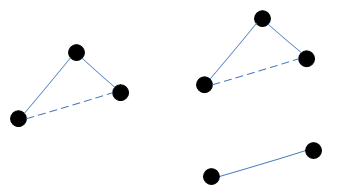
Def. tree คือ กราฟที่ Connected และไม่มี Cycle
Thm. ข้อความข้างล่างนี้ให้ G มี n node
- 1) G Connected
- 2) G ไม่มี Cycle
- 3) G มีเส้นเชื่อม n-1 เส้น
- 2 ข้อใดๆ จะ imply ข้อที่ 3 และ imply ว่า G เป็น tree
- 2 ข้อใดๆ จะ imply ข้อที่ 3 และ imply ว่า G เป็น tree
Proof (1,2-->3)
- (I) ถ้า G Connected,G จะต้องมีอย่างน้อย n-1 edge
- (II) ถ้า G มี edge G มี Cycle
- เพราะฉะนั้น G ไม่มี Cycle , G มี edge