ผลต่างระหว่างรุ่นของ "01204512/congestion1"
Jittat (คุย | มีส่วนร่วม) |
Jittat (คุย | มีส่วนร่วม) |
||
| แถว 41: | แถว 41: | ||
=== การปรับระยะทางแบบเชิงเส้น === | === การปรับระยะทางแบบเชิงเส้น === | ||
| − | เราจะปรับความยาวของ edge ตาม congestion ของ edge นั้น กล่าวคือ ในแต่ละรอบที่เราหาเส้นทางที่สั้นที่สุดเราจะให้ <math>\ell(e)=c(e)</math> สำหรับทุก ๆ เส้นเชื่อม | + | เราจะปรับความยาวของ edge ตาม congestion ของ edge นั้น กล่าวคือ ในแต่ละรอบที่เราหาเส้นทางที่สั้นที่สุดเราจะให้ <math>\ell(e)=c(e)</math> สำหรับทุก ๆ เส้นเชื่อม เราจะทยอยเพิ่ม path เข้าไปในระบบจนกว่าระบบจะ "นิ่ง" |
| + | |||
| + | เมื่อใดที่เราจะเรียกว่าระบบ "นิ่ง"? ถ้าเราเลือกเส้นทางใด เราจะเพิ่มค่า congestion ให้กับ edge บน เส้นทางนั้น ทำให้ในรอบต่อไปเวลาเราจะเลือกเส้นทางที่สั้นที่สุด เราจะเลือกได้เส้นทางอื่น ในที่นี้เราจะพิจารณาแบบง่ายไปก่อนว่า เราจะเรียกว่าระบบนิ่ง เมื่อความยาวของ path ใด ๆ เท่ากัน | ||
| + | |||
| + | สังเกตว่าในกรณีนี้ ความยาวของ edge ใน path ที่มี edge เดียว (เส้นล่างสุด) จะต้องยาวเท่ากับเส้นอื่น ๆ ทั้ง <math>k</math> เส้น นั่นคือเราจะได้ว่า | ||
| + | |||
| + | <math> | ||
| + | c(e_1)=2\cdot c(e_2)=3\cdot c(e_3)=\cdots = k\cdot c(e_k) | ||
| + | </math> | ||
รุ่นแก้ไขเมื่อ 17:09, 3 กรกฎาคม 2555
- หน้านี้เป็นเอกสารประกอบวิชา 01204512 เนื้อหาจาก http://www.cs.berkeley.edu/~satishr/cs270/sp12/ lecture 1
- เนื้อหายังไม่เรียบร้อย... น่าจะแก้เสร็จภายในวันนี้ (หลังเลิกเรียน)
ปัญหา congestion minimization
ให้กราฟ และเซตของคู่ของจุดยอด จำนวน คู่ เราต้องการหาเซตของเส้นทาง (path) ที่เชื่อมจุดยอดแต่ละคู่ โดยต้องการทำให้จำนวน path ที่ผ่านเส้นเชื่อมใด ๆ มีค่าน้อยที่สุด (เราจะเรียกจำนวนผ่านที่ผ่านเส้นเชื่อมใด ๆ ว่าเป็น congestion ของเส้นเชื่อมนั้น)
คำตอบใด ๆ ของปัญหานี้ คือเซตของ path จำนวน เส้น แต่เราต้องการให้ path เหล่านี้ กระจายกันไป path เหล่านี้ทำให้เกิด congestion บนเส้นเชื่อม เป้าหมายที่เราต้องการจะทำให้มีค่าต่ำสุดของปัญหานี้คือ congestion ที่มากที่สุดบนเส้นเชื่อมใด ๆ
ถ้าเขียนให้ชัดเจนก็คือ เราต้องการจะ:
หา path:
ที่ เชื่อมระหว่าง กับ สำหรับ
เพื่อจะ minimize
เมื่อ คือจำนวน path ที่ผ่านเส้นเชื่อม
ปัญหานี้อาจจะยากสักหน่อย เราจะพิจารณาปัญหาที่ง่ายลง แทนที่เราจะ minimize ค่า congestion ที่สูงที่สุด เราจะ minimize ค่าเฉลี่ยของ congestion กล่าวคือ เราจะ:
minimize , เมื่อ แทนจำนวนเส้นเชื่อม
สังเกตว่าผลรวมของ congestion บนทุก ๆ เส้นเชื่อมนั้น เท่ากับผลรวมของความยาวของทุก ๆ path ดังนั้นเป้าหมายที่เราต้องการจะ minimize คือ
ซึ่งปัญหานี้ เราสามารถแก้ได้โดยง่าย โดยใช้อัลกอริทึมสำหรับ shortest path
สังเกตเพิ่มเติมว่า ค่าคำตอบของปัญหา average congestion minimization นี้ เป็น lower bound ของค่าของคำตอบของปัญหา congestion minimization (เพราะอะไร?) ดังนั้น ถ้าเราจะแก้ปัญหา congestion minimization โดยการใช้วิธีของปัญหาแรกเลยจะได้หรือไม่?
ถ้าเราพิจารณาให้ดี เราจะพบว่า มีตัวอย่างง่าย ๆ ที่ผลลัพธ์ที่ได้ มี congestion เท่ากับ ในขณะที่คำตอบที่ดีที่สุดให้ congestion แค่ 1 เท่านั้น
สังเกตว่าทุก ๆ path จะพยายามไปใช้เส้นทางที่สั้นที่สุดพร้อม ๆ กันหมด เราจะพยายามแก้ปัญหานี้โดยการทำให้เส้นทางที่สั้นที่สุดมีความ "น่าใช้" ลดลงเรื่อย ๆ เราจะทดลองหลาย ๆ แบบ
การปรับระยะทางแบบเชิงเส้น
เราจะปรับความยาวของ edge ตาม congestion ของ edge นั้น กล่าวคือ ในแต่ละรอบที่เราหาเส้นทางที่สั้นที่สุดเราจะให้ สำหรับทุก ๆ เส้นเชื่อม เราจะทยอยเพิ่ม path เข้าไปในระบบจนกว่าระบบจะ "นิ่ง"
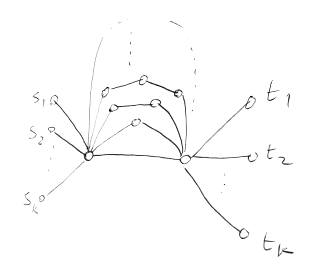
เมื่อใดที่เราจะเรียกว่าระบบ "นิ่ง"? ถ้าเราเลือกเส้นทางใด เราจะเพิ่มค่า congestion ให้กับ edge บน เส้นทางนั้น ทำให้ในรอบต่อไปเวลาเราจะเลือกเส้นทางที่สั้นที่สุด เราจะเลือกได้เส้นทางอื่น ในที่นี้เราจะพิจารณาแบบง่ายไปก่อนว่า เราจะเรียกว่าระบบนิ่ง เมื่อความยาวของ path ใด ๆ เท่ากัน
สังเกตว่าในกรณีนี้ ความยาวของ edge ใน path ที่มี edge เดียว (เส้นล่างสุด) จะต้องยาวเท่ากับเส้นอื่น ๆ ทั้ง เส้น นั่นคือเราจะได้ว่า