ผลต่างระหว่างรุ่นของ "204512-53/lecture7"
ไปยังการนำทาง
ไปยังการค้นหา
Kiatchumpol (คุย | มีส่วนร่วม) |
Kiatchumpol (คุย | มีส่วนร่วม) |
||
| แถว 50: | แถว 50: | ||
<math>D(v) <- D(u) + l(u,v)</math> | <math>D(v) <- D(u) + l(u,v)</math> | ||
<math>p(v) <- u</math> | <math>p(v) <- u</math> | ||
| + | |||
| + | Ford's algorithm -> ทำ labeling step ไปเรื่อยๆ | ||
| + | |||
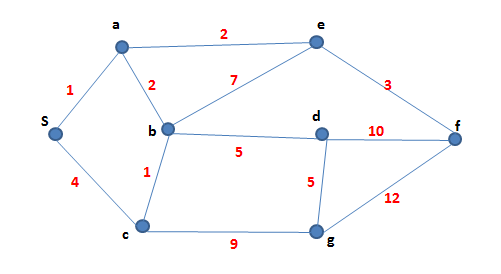
| + | ตัวอย่าง | ||
| + | |||
| + | มี Graph | ||
| + | [[ไฟล์:lecture7_figure3.png]] | ||
| + | |||
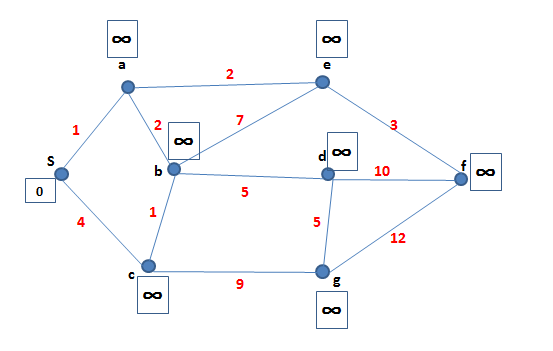
| + | Step เริ่มต้น <math>D(s) = 0</math> และ <math>D(u)</math> ของโหนดอื่นๆ มีค่าเป็น <math>\infty</math> | ||
| + | [[ไฟล์:lecture7_figure4.png]] | ||
รุ่นแก้ไขเมื่อ 10:02, 29 สิงหาคม 2553
จดบันทึกคำบรรยายโดย:
5314550032 นาย กิตติกานต์ ดวงประภา
5314550041 นาย เกียรติชุมพล สุทธิศิริกุล
5314550059 นาย ฉนานนท์ ตันสกุล
Shortest Paths
มี โดยที่
มี : โดยที่
ให้ สำหรับ ใดๆ แทนระยะทางที่สั้นที่สุดจาก ไป
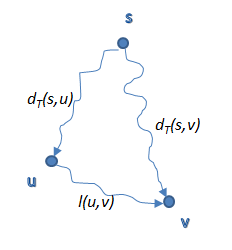
Lemma: ถ้าให้ เป็นระยะทางจาก ไป บน แล้ว จะเป็น shortest path tree ก็ต่อเมื่อ(if and only if) สำหรับทุกๆ เส้นเชื่อม
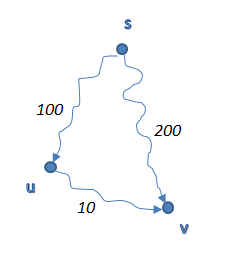
พิจารณาตัวอย่าง
จากรูปข้างบน ในที่นี้ ไม่ใช่ shortest path แล้ว ถ้าเราอยากทราบ shortest path เราก็บอก parent ของ ให้วิ่งไปหา shortest path ทางอื่น อย่าวิ่งผ่านมาที่ (นี่คือการ update shortest path)
Framework ของการหา shortest path
- ทุกๆ โหนดเก็บ parent , โหนด เก็บ ที่เป็น parent ใน candidate shortest path tree
(เริ่มต้น)
- ทุกๆ โหนด เก็บ ซึ่งแทนระยะทางที่สั้นที่สุด"เท่าที่ทราบ" จาก ไป
(เริ่มต้น)
LABELING STEP:
เลือกเส้นเชื่อม ที่ จากนั้น
Ford's algorithm -> ทำ labeling step ไปเรื่อยๆ
ตัวอย่าง