204512-53/lecture11

'จดบันทึกคำบรรยายโดย:

 นายชัชพล      นุโยค รหัส 5214550049 (Part I)
 นายสุรเดช      วัฒนอุดมโรจน์ รหัส 5214550324 (Part I)
 นายชัยณรงค์   เหมือนรุ่ง รหัส 5214550057 (Part II)
 นายศศิน         เทียนดี รหัส 5214550278 (Part II)
 น.ส.นันทณัฏฐ์ ภูทอง รหัส 5214550171 (Part II)
 น.ส.ชนาพร    คุรุรัตน์พันธ์  รหัส 5214550031 (Part II)

---

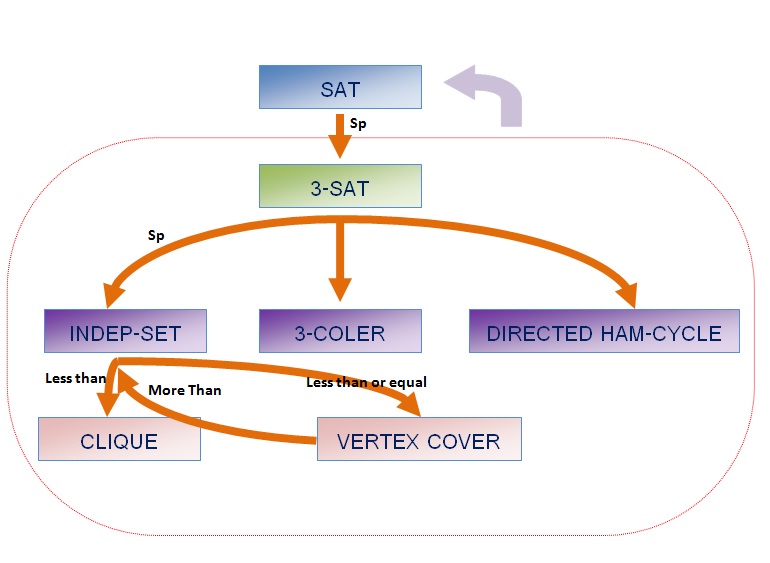
Part I NP Completeness

---

NP: Non-deterministic Polynomial time คือ เซตของ Algorithm ที่ไม่สามารถแก้ไขปัญหาได้ในเวลาที่เป็น polynomial โดยการนิยามเซตของปัญหาเพื่อประโยชน์ในการเปรียบเทียบระดับความยาก-ง่ายของ Algorithm ซึ่งเซตของปัญหาสามารถแบ่งเป็นเซต P, NP, NP-hard และ NP-complete

ในการเปรียบเทียบ Algorithm ใดๆ เราจะทำการพิจารณา Algorithm ว่าจัดอยู่ในเซตของปัญหาใด โดยใช้เทคนิคการลดรูปของปัญหา (Reduction) ว่าเป็นกลุ่มเดียวกับปัญหาที่อยู่ในเซตหรือไม่ ถ้าอยู่ในกลุ่มเดียวกันจะกล่าวว่า Algorithm มีความยากเท่ากัน ความยาก คือ มี Algorithm ที่มีประสิทธิภาพแก้ไขปัญหาหรือไม่

ปัญหา A สัมพันธ์ ปัญหา B

ปัญหา A ไม่ยากไปกว่า ปัญหา B

ปัญหา A ปัญหา B

โดยมีความหมายว่า ถ้ามี Algorithm ที่สามารถแก้ปัญหา B ได้ ปัญหา A ก็จะสามารถแก้ได้เช่นกัน

---

ปัญหาที่ 1 : Independent Set เป็นปัญหากลุ่ม Decision Problem

นิยาม : ให้ Undirected graph G = (V, E) จะกล่าวว่า I V เป็น Independent Set ก็ต่อเมื่อ สำหรับทุกๆโหนด U,V I, U V ไม่มีเส้นเชื่อมระหว่าง U และ V

ปัญหา : ให้กราฟ G = (V, E) และ integer k, มี Independent set ขนาด ≥ k หรือไม่

ในภาพทำการเลือกโหนด (k) เท่ากับ 1 จะกล่าวว่ามี Independent set ขนาด 1

สามารถนำไปใช้แก้ปัญหา หาคนที่ไม่รู้จักกันในห้อง หรือ การเปิด-ปิดไฟแดงที่แยก

---

ปัญหาที่ 2 : Vertex Cover

นิยาม : C V เป็น Vertex Cover ก็ต่อเมื่อ (U,V) E,U C หรือ V C

ปัญหา : ให้กราฟ G = (V, E) และ จำนวนเต็ม k ถามว่ามี vertex cover ขนาด ≤ k หรือไม่

---

ถ้าสมมติให้ Independent Set Vertex Cover

Lemma : พิจารณาเซต A V ใดๆ ให้ A เป็น imdenpendent set โดย V-A เป็น Vertec Cover

Proof : Indenpendent set Vertex Cover

นิยาม : ปัญหา A เป็น Polynomial time เพื่อลดปัญหา B ถ้ามี Algorithm T ที่ทำงานใน Polynomial time สำหรับทุกๆ instance X ของ A จะได้ T(x) เป็น instance ของ B

X' = T(x) เป็น instance ของ B และ |X'| = Poly (|X|)

   ถ้า x เป็น instance ตอบ "Yes" ใน A
  => x' เป็น instance ตอบ "Yes" ใน B

   ถ้า x เป็น instance ตอบ "No" ใน A
  => x' เป็น instance ตอบ "No" ใน B

Lemma : ถ้า A B และมี Algorithm ที่แก้ปัญหา B ได้ใน Polynomial time จะมี Algorithm ที่แก้ปัญหา A ใน Polynomial time ได้ด้วย

Proof : ให้ M เป็น Polynomial time Algorithm ที่แก้ปัญหา B จะได้ว่า A B นั้นคือ มี Polynomial time Algorithm T ที่ instance x ของ A x' = T(x) มีขนาด poly(|x|) และคำตอบของ x ในปัญหา A ตรงกับของ x' ในปัญหา B

สำหรับ Algorithm M' ดังนี้

  M'(x) :
  x' = T(x)
  return M(x')

แต่เนื่องจาก |x'| = poly(|x|) ดังนั้น เวลาในการคำนวณ M(x')คือ poly(|x'|) = poly(poly(|x|)) = poly(|x|)

จากนิยาม M'(x) เป็นคำตอบของ x ใน A เหลือแต่ต้องตรวจสอบว่า M' ทำงานใน Polynomial time หรือ poly(|x|)

---

Part II

พิจารณา กราฟ G = (V,E) , C  V เรียกว่า Clique
ก็ต่อเมื่อ  u,v  C ที่ us
(u,v) E

CLIQUE

ให้กราฟ G = (V,E) และจำนวนเต็ม K
กราฟ G clique = (V,E') เป็น Complement ของ G
ถ้า
 (u,v) E <--> (u,v) E'

Lemma  กราฟ G = (V,E) มี Independent Set ขนาด K ใน G clique = (V,E') มี Clique ของ K
Proof (->)
       ให้ I เป็น Independent Set ขนาด K ใน G
       พิจารณาโหนด u,v  I ใดๆ ที่ uv เนื่องจาก ณ เป็น Indep ใน G(u,v) E
       จากนิยามของ G clique , จะได้ว่า (u,v)  E clique
       ดังนั้นทุกๆ u,v  I ที่ uv ,(u,v) E Clique
       นั้นคือ I เป็น Clique ใน  G clique
              เนทาองจาก |I| = K , G plus  มี Clique ขนาด k 9k,9hv'dki

Proof (<-)

SAT

  Note : Clause ที่เป็นการ OR กับของตัวแปรหรือนิเสธของตัวแปร เรียกว่า Disjunction ตัวอย่างเช่น $(X_{1}\lor X_{2})$

ปัญหา 3-Satisfiability (3-SAT)

รับค่า CNF Formula ${\boldsymbol {\phi }}$ ที่แต่ละ clause มีตัวแปร $\leq$ 3 ตัว
ถามว่าทำให้ ${\boldsymbol {\phi }}$ เป็นจริงได้หรือไม่ ?

กรณี $3-SAT\leq _{p}SAT$

ในกรณีนี้เป็นจริงอยู่แล้วเพราะ 3-SAT เป็นกรณีเฉพาะของ SAT แต่เราต้องการพิสูจน์ว่า

$SAT\leq _{p}3-SAT$

plan: แสดงว่าสำหรับ CNF ${\boldsymbol {\phi }}$ ใดๆ มีวิธีการสร้าง ${\boldsymbol {\psi }}$ ที่เป็น 3-CNF ที่

ถ้า ${\boldsymbol {\phi }}\in SAT,{\boldsymbol {\psi }}\in 3-SAT$

และถ้า${\boldsymbol {\phi }}\notin SAT,{\boldsymbol {\psi }}\notin 3-SAT$

ในเวลา Polynomial time
ตัวอย่างที่ 1

${\boldsymbol {\phi }}=(X_{1}\lor X_{2}\lor \neg X_{3}\lor X_{4})$

ให้ใช้วิธีการเพิ่มตัวแปร $Z_{1}$ จะเปลี่ยนไปอยู่ในรูป

${\boldsymbol {\psi }}=(X_{1}\lor X_{2}\lor Z_{1})\land (\neg X_{3}\lor X_{4}\lor \neg Z_{1})$

ตัวอย่างที่ 2

${\boldsymbol {\phi }}=(X_{1}\lor X_{2}\lor \neg X_{3}\lor X_{4}\lor \neg X_{5})$

ให้ใช้วิธีการเพิ่มตัวแปร $Z_{1},Z_{2}$ จะเปลี่ยนไปอยู่ในรูป

${\boldsymbol {\psi }}=(X_{1}\lor X_{2}\lor \neg Z_{1})\land (Z_{1}\lor \neg X_{3}\lor \neg Z_{2})\land (Z_{2}\lor X_{4}\lor \neg X_{5})$

  Note : การเติมตัวแปร Z จะต้องเติมแล้วทำให้ค่าความจริงของ ${\boldsymbol {\phi }}$ equivalence กับค่าความจริงของ ${\boldsymbol {\psi }}$

ปัญหา Independent Set

นิยาม ให้ Undirected graph G = (V,E) จะกล่าวว่า $I\subseteq V$ เป็น Independent Set ถ้าทุกๆ คู่ของโหนด $U,V\subseteq I$ ไม่มีเส้นเชื่อมกัน

ปัญหา Independent set ให้กราฟ G = (V,E) และ integer k, มี Independent set I ใน G ที่ $|I|\geq k$ หรือไม่ ?
เราสามารถลดรูปปัญหา 3-SAT ไปเป็นปัญหา Independent set ได้

$3-SAT\leq _{p}$Independent set
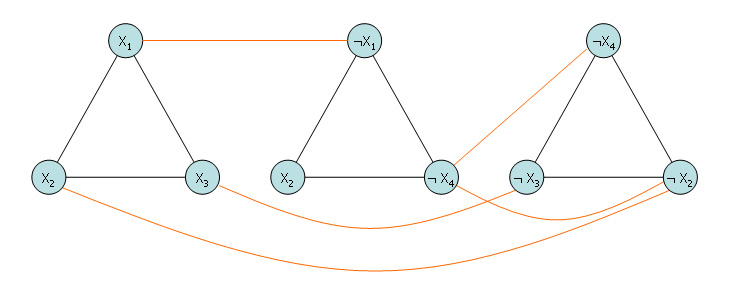
ให้ 3-CNF Formular ที่ประกอบด้วย clauses $C_{1},C_{2},...,C_{m}$ จะสร้างกราฟ G ดังนี้

• พิจารณา clause C₁ สร้างโหนด V₁₁,V₁₂,V₁₃ สำหรับแต่ละตัวแปรหรือนิเสธของตัวแปรใน C₁
  
• เพิ่มเส้นเชื่อม (V₁₁,V₁₂),(V₁₁,V₁₃),(V₁₃,V₁₁)
  
• สำหรับโหนดที่แทนตัวแปรกับนิเสธของตัวแปรเดียวกับเพิ่มเส้นเชื่อมระหว่างโหนดเหล่านี้
  
  

$(X_{1}\lor X_{2}\lor X_{3})\land (\neg X_{1}\lor X_{2}\lor \neg X_{4})\land (X_{4}\lor \neg X_{3}\lor \neg X_{2})$

ถ้า ${\boldsymbol {\phi }}\in 3-SAT$ จะมี independence set ขนาด m ใน G

ถ้ามี independence set ขนาด m ใน G $\Rightarrow {\boldsymbol {\phi }}\in 3-SAT$

Class NP (Non-deterministic Polynomial time)

ปัญหา L จะอยู่ใน $\mathbb {N} \mathbb {P}$ ถ้ามี polynomail time algorithm V ที่ $\forall x\in L$ มี certificate P ที่ $\left|P\right|=poly\left(\left|x\right|\right)$ และ V(x,p) = 1
แล้ว $\forall x\in L$, $V\left(x,P\right)=1$ และ $\forall x\notin L$, $V\left(x,P\right)=0$
สรุป ปัญหา NP คือกลุ่มปัญหาที่สามารถตรวจคำตอบได้ภายใน polynomial time ซึ่งปัญหาง่ายๆ ก็อยู่ใน NP ด้วย
ปัญหา NP-Complete : ปัญหา $X\in$NP-Complete ถ้าสำหรับทุกปัญหา $Y\in NP$ แล้ว $Y\leq _{p}X$
Cook-Lavin Theorem -> Proof ว่า SAT เป็น NP-Complete

$SAT\leq _{p}3-SAT\leq _{p}Independentset$

สรุป ทั้ง 3-SAT และ independent set เป็น NP-Complete

  Note : Steps ในการแสดงว่าปัญหา X เป็น NP-Complete คือ 

   1. Proof ว่า $X\in NP$ 2. Proof ว่ามีปัญหา Y ที่เป็น NP-Complete ที่ $Y\leq _{p}X$

ปัญหา Vertex Cover

เซต $\mathbf {C}$ เป็น Vertex Corver ของกราฟ $\mathbf {G} =(\mathbf {V} ,\mathbf {E} )$ ถ้า $C\subseteq V$ และทุกๆ edge $(U,V)\in E,U\in C$ หรือ $V\in C$
ปัญหา Vertex Corver จะให้กราฟ $\mathbf {G}$, integer k ถามว่า $\mathbf {G}$ มี vertex corver ที่มีขนาด $\leq$ k หรือไม่ ?<br\>

• Independent set $\leq _{p}$ Vertex Corver<br\>
  • Lemma พิจารณากราฟ $\mathbf {G} =(\mathbf {V} ,\mathbf {E} ),I\subseteq V$ เป็น Independent Set
    

(รูปภาพ)
รับกราฟ $\mathbf {G}$ ถามว่ามี independent set $\leq$ k ? สร้าง instance ของ Vertex Corver ที่มีกราฟ $\mathbf {G}$ ถามว่าใน $\mathbf {G}$ มี Vertex Corver ขนาด n-k หรือไม่ ? เมื่อ n = จำนวนโหนดใน $\mathbf {G}$<br\>
Vertex Corver เป็น NP Complete เนื่องจากสามารถตรวจได้ว่ากราฟมี Vertex Corver ขนาดไม่เกิน k โดยใช้ Certificate เป็น Vertex Corver นั้น $\Rightarrow VC\in NP$

ปัญหา 3-Color บทเรียนเก่า(เพิ่มเติม)

ให้กราฟ $\mathbf {G}$ ต้องการกำหนดสีให้กับแต่ละโหนด โดยที่คู่ของโหนดที่มีเส้นเชื่อมถึงกันห้ามใช้สีเดียวกัน สามารถทำได้โดยใช้สี $\leq$ 3 สีหรือไม่ ?

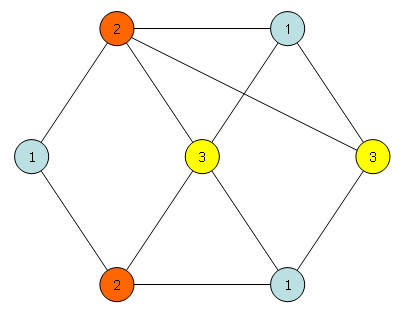
จะแสดงว่า 3-Color เป็น NP Complete
1. แสดงว่า $3-Color\in NP$

ใช้การกำหนดสีให้กับแต่ละโหนดเป็น Certificate ตรวจว่า

1) ใช้สีไม่เกิน 3 สี

2)ไม่มี edge เติมโหนดที่มีปัญหาทำได้ polynomial time

ซึ่งสามารถทำได้ใน polynomial time

2. แสดงว่า $3-Color\leq _{p}3-SAT$

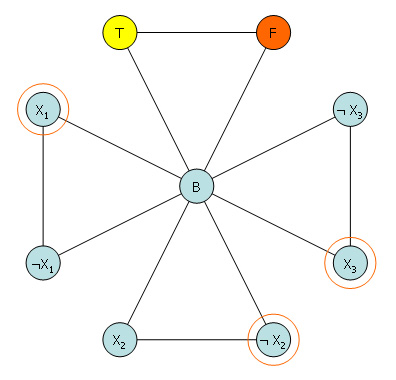
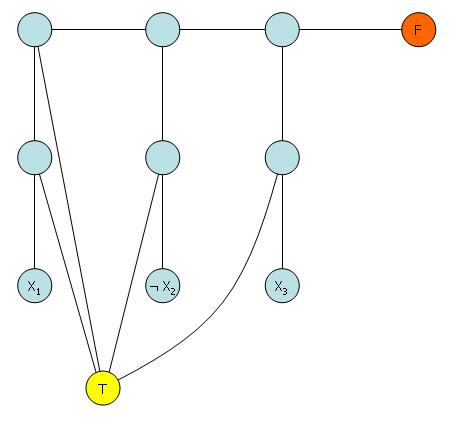
กำหนดโหนด 3 โหนดแทนสี 3 สี จากนั้นสร้างกราฟดังนี้

ถ้าให้ clause $X_{1}\lor \neg X_{2}\lor X_{3}$ ต้องสร้างกราฟให้มีตัวใดตัวหนึ่งเป็นจริงและอีก 2 ตัวเป็น false ได้กราฟดังนี้

กราฟนี้จะบังคับให้ต้องมีตัวใดตัวหนึ่งเป็น True นั่นคือ $3-Color\leq _{p}3-SAT$