ผลต่างระหว่างรุ่นของ "204512/บรรยาย 5"
| แถว 1: | แถว 1: | ||
{{หัวคำบรรยาย|204512}} | {{หัวคำบรรยาย|204512}} | ||
'''จดบันทึกคำบรรยายโดย:''' | '''จดบันทึกคำบรรยายโดย:''' | ||
| − | '' | + | '' ทวีศักดิ์ อัชรางกูร รหัส : 50653807'' |
== ทบทวน == | == ทบทวน == | ||
=== Graph === | === Graph === | ||
รุ่นแก้ไขปัจจุบันเมื่อ 15:44, 22 กันยายน 2550
บันทึกคำบรรยายวิชา 204512 นี้ เป็นบันทึกที่นิสิตเขียนขึ้น เนื้อหาโดยมากยังไม่ผ่านการตรวจสอบอย่างละเอียด การนำไปใช้ควรระมัดระวัง
จดบันทึกคำบรรยายโดย: ทวีศักดิ์ อัชรางกูร รหัส : 50653807
เนื้อหา
ทบทวน
Graph
เซตของโหนด
เซตของเส้นเชื่อม
ตัวอย่าง

- จะกล่าวว่าเส้นเชื่อม (u,v) ติดกับโหนด u และ v
- u และ v เป็นจุดปลายของเส้นเชื่อม (u,v)
- degree ของโหนดใดๆ คือ จำนวนเส้นเชื่อมที่ติดกับโหนดนี้
- path คือ ลำดับของโหนด ที่
- สำหรับทุกๆ เรียก เป็นจุดเริ่มต้น , เป็นจุดสิ้นสุด
Thm
- ถ้ากราฟ มี m edge ให้ deg(u) แทน degree ของโหนด u
Def
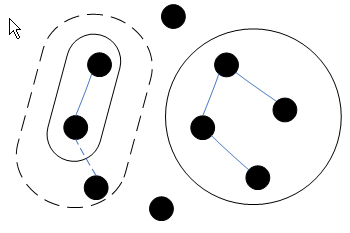
- กราฟ G Connected ถ้าทุกๆ โหนด u มี path ไปยังทุกๆ โหนด v
เป็น connected coponent ใน G ตัว ทุกๆ โหนดใน C มี path ไปถึงทุกๆ โหนดใน C และ
ไม่มี path ไปยังโหนด v อื่นๆ ที่
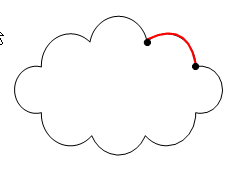
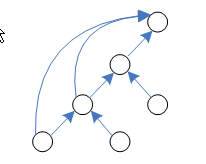
Cycle คือ path ที่มีจุดเริ่มต้นเป็นจุดเดียวกับจุดสิ้นสุด ดังรูป

Def. tree คือ กราฟที่ Connected และไม่มี Cycle
Thm. ข้อความข้างล่างนี้ให้ G มี n node
- 1) G Connected
- 2) G ไม่มี Cycle
- 3) G มีเส้นเชื่อม n-1 เส้น
- 2 ข้อใดๆ จะ imply ข้อที่ 3 และ imply ว่า G เป็น tree
- 2 ข้อใดๆ จะ imply ข้อที่ 3 และ imply ว่า G เป็น tree
Proof (1,2-->3)
- (I) ถ้า G Connected,G จะต้องมีอย่างน้อย n-1 edge
- (II) ถ้า G มี edge G มี Cycle
- เพราะฉะนั้น G ไม่มี Cycle , G มี edge
Spanning tree
- ให้กราฟ G = (V,E) เรียก tree ว่าเป็น spanning tree ถ้า
ปัญหา minimum spanning tree
- ให้กราฟ G = (V,E) พร้อมด้วยฟังก์ชั่นน้ำหนัก w บนเส้นเชื่อม ต้องการหา spanning tree
T ที่ผลรวมของ weight บนเส้นเชื่อมน้อยที่สุด

Greedy framework
- ทุกๆ เส้นเชื่อมจะมี
- ไม่มีสี(unknow)
- สีน้ำเงิน(accept)
- สีแดง(reject)
Invariant
- จะมี minimum spanning tree ที่มีเส้นเชื่อมสีน้ำเงินทั้งหมดและไม่มีเส้นเชื่อมสีแดง
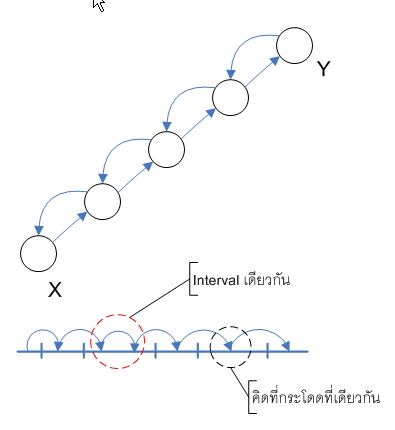
cut คือ partition ของเซตของโหนดออกเป็นสองส่วน

- เส้นเชื่อม e ข้าม Cut ถ้าจุดปลายด้านหนึ่งของ edge อยู่ใน X อีกช่วงอยู่ใน
Blue Rule และ Red Rule
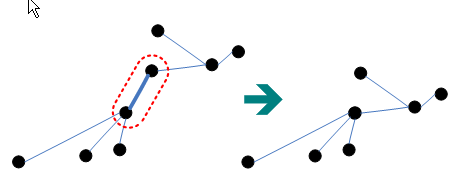
- blue rule พิจารณา Cut ใดๆ ที่ไม่มีเส้นเชื่อมสีน้ำเงินข้าม cut นั้น เลือกเส้นเชื่อมที่มีน้ำหนักน้อยสุด และให้ e มีสีน้ำเงิน
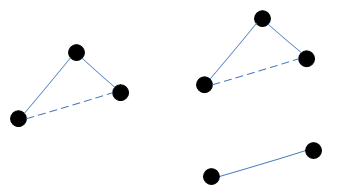
- red rule พิจารณา Cycle ใดๆ ที่ไม่มี edge สีแดงอยู่เลือกเส้น e ที่น้ำหนักมากสุดให้ e มีสีแดง
- สามารถทำตาม blue rule/red rule ได้จนกระทั่งทุกๆ edge มีสีและตลอดการทำงาน invariant เป็นจริง
Proof
- เมื่อเริ่มต้น (ทุกๆ edge ไม่มีสี)ทุกๆ เส้นเชื่อมไม่มีสี invariant เป็นจริง
- assume ว่า invariant จริงมี minimum spanning tree ตาม invariant
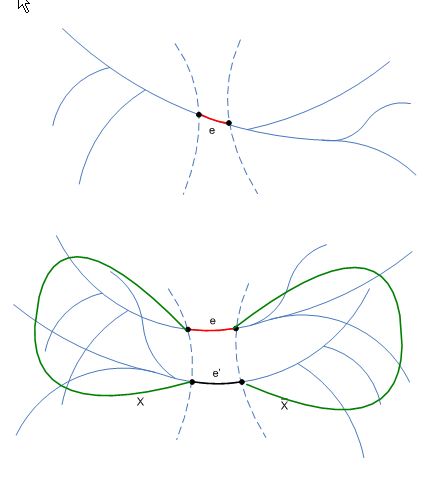
blue rule ถ้า apply blue rule กับ edge e,บน cut ถ้า assume ว่า ดังรูป

- เนื่องจาก T เป็น Spanning tree มี path จาก u ไป v บน T
path นี้จะต้องข้าม จะมี ที่ข้าม cut
Claim
- ให้ T' เป็น Minimum Spanning Tree
Proof
- 1)T' ไม่มี Cycle T' เป็น tree และวิ่งผ่านทุกโหนดในกราฟ
- 2)T' Connected เป็น tree และวิ่งผ่านทุกโหนดในกราฟ
- เราทราบว่า e มีน้ำหนักน้อยสุดใน cut
- น้ำหนัก น้ำหนักของ e' imply ว่า น้ำหนักของ น้ำหนักของ T
- นั่นคือ invariant ยังจริงอยู่หลังทำ Blue rule
- ให้ทำ red rule ให้ edge เป็นสีแดงบน Cycle C
- ถ้า assume ดังรูป
- พิจารณา
- น้ำหนักของ น้ำหนักของ T
- นอกจากนี้ T' เป็น spanning tree ดังนั้นหลังจากการทำ red rule,จะมี minimum spanning tree
T' ที่มี edge สีน้ำเงินทั้งหมด และไม่มี edge สีแดงเลย แสดงว่า invariant จริงอยู่
Blue Forest
Buruvka
- ห้าม edge weight ซ้ำกัน
- ทำงาน
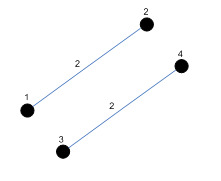
- 2,1,2 และ 2,3,4
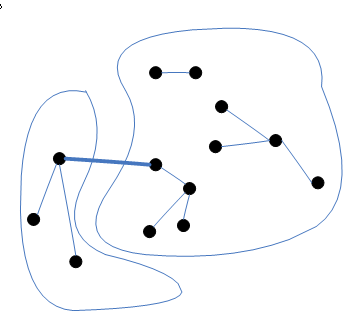
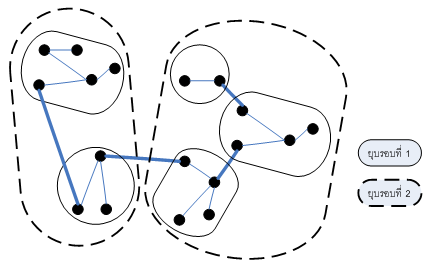
- เริ่มต้นเรามีกราฟ ทุกๆโหนดมองรอบตัวเองและเลือก edge ที่น้ำหนักน้อยที่สุดออกมา และทำเช่นนี้จนกว่าจะเชื่อมทุกโหนดได้ ดังรูป
- Comment ข้อเสียของวิธีนี้คือ กรณีที่ edge เท่ากันจะทำให้เกิด Cycle เพราะว่าการเลือกแต่เฉพาะส่วนที่ใกล้ตัวเองไม่ได้คำนึงถึงตัวอื่น
Prim's Algorithm
- เลือกตัวที่ใกล้ที่สุดออกไปเรื่อยๆ จนกระทั่งเป็น tree
Kruskal's Alogorithm
- หลักคือ เอา edge มาเรียงกันจากน้อยไปมากหลังจากนั้นก็โยนเข้าไปเรื่อยๆให้ไม่เกิด Cycle
จะเกิดปัญหาก็ต่อเมื่อโยน edge เข้าไปแล้วทำให้เกิด Cycle ยึดหลักการ Sort edge
- การทำงาน
Union-Find
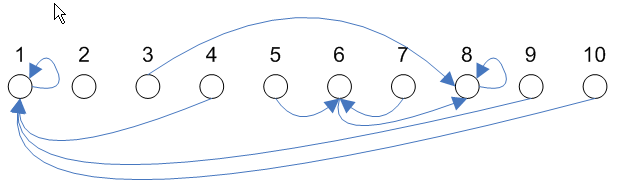
- ยึดหลักการทำงานของ Kruskal ซึ่งแต่ละโหนดเป็นอิสระต่อกันซึ่งโครงสร้างพื้นฐาน คือ Set ดังรูป
- ถ้าหากไม่อยู่ใน Set เดียวกันก็จับมา Union กัน
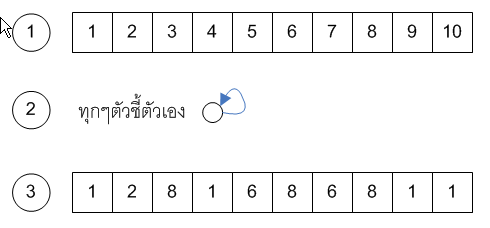
- element n ตัว มี Set s {{1},{2},{3},....{n}}
- find(x) คือ identity ของ set ที่มี x อยู่
- union(x) รวม set ที่มี x กับ y เข้าด้วยกัน
- ดังรูป
- make set(x)
- parent(x)<--x,rank(x)<---0
- while(parent(x)<>x)
- x<--parent(x)
- return x
- while(parent(x)<>x)
- union(x,y)
- <-- find(x)
- <-- find(y)
- parent<--
- if rank < rank
- parent<--
- else
- parent<--
- if rank= rank
- rank<-- rank + 1
- if rank= rank
- parent<--
- if rank < rank
- Observation 1
- ถ้า parent(x)<>x,rank(x)< rank(parent(x))
- Observation 2
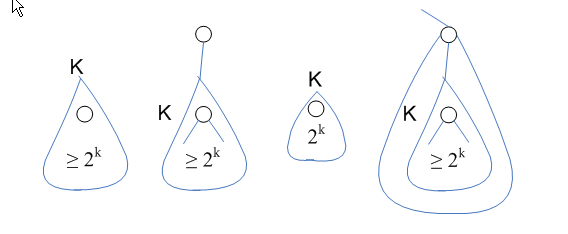
- สำหรับ tree ที่ root มี rank k
- tree มี node โหนด
- Observation 3
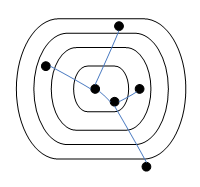
- โหนดมี rank k มีไม่เกิน โหนด ดังภาพ
- Find ทำงานในเวลา O(m log* n)
Path Compress
- แนวคิด log*n ดังรูป
- Algorithm ของ Path Compress
- if parent(x)<>x
- parent(x) = find(parent(x))
- return parent(x)
- if parent(x)<>x
อธิบาย
- {1},{2},{3,4},{5,6,..,16},{17,..},....,{k+1,..,},....,{65537,} ดังรูปประกอบด้านล่าง
- {1},{2},{3,4},{5,6,..,16},{17,..},....,{k+1,..,},....,{65537,} ดังรูปประกอบด้านล่าง
- จะเขียนสมการได้ว่า
- การทำ find m รอบ