ผลต่างระหว่างรุ่นของ "Closet pairs and merge sort"
Aoy (คุย | มีส่วนร่วม) |
Aoy (คุย | มีส่วนร่วม) |
||
| แถว 4: | แถว 4: | ||
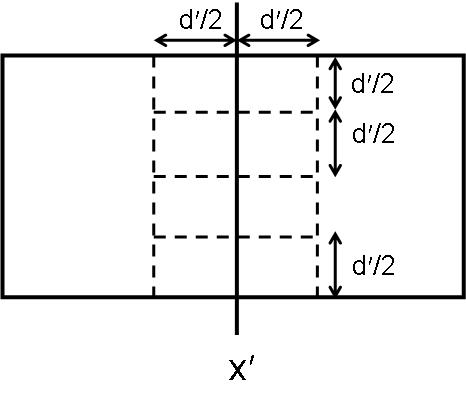
ข้อสังเกต 2: ถ้าสมมติดว่าแบ่งแถบ <math> [x' - d', x' + d'] \,</math> ออกเป็นช่อง ๆ แต่ละช่องมีความกว้างและความยาวเป็น <math> d'/2 \,</math> ดังภาพ | ข้อสังเกต 2: ถ้าสมมติดว่าแบ่งแถบ <math> [x' - d', x' + d'] \,</math> ออกเป็นช่อง ๆ แต่ละช่องมีความกว้างและความยาวเป็น <math> d'/2 \,</math> ดังภาพ | ||
| + | |||
| + | [[ไฟล์:devide.JPG]] | ||
| + | |||
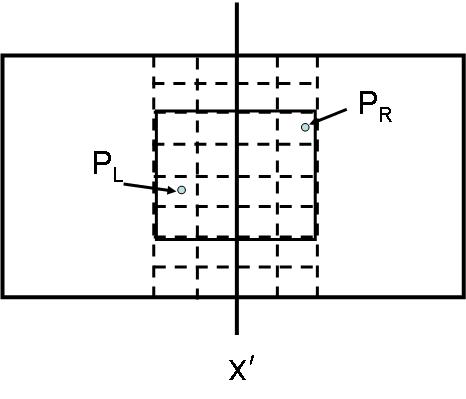
| + | ข้อสังเกต 3: ถ้ามีจุด <math> P_L, P_R \,</math> ที่อยู่ใกล้กัน เป็นระยะห่างน้อยกว่า <math> d' \, </math> และจะมีตารางขนาด 4 x 4 ที่แต่ละช่องมีความกว้าง <math> d'/2 \,</math> ที่ <math> P_L, P_R \,</math> อยู่ในตารางนั้นเสมอ ดังภาพ | ||
| + | |||
| + | [[ไฟล์:4mul4.JPG]] | ||
| + | |||
| + | ข้อสังเกต 4: ถ้านำเซต <math>L \, </math> และเซต <math>R \, </math> มารวมกัน แล้วคัดเฉพาะจุดที่อยู่ในแถบ <math> [x' - d', x' + d'] \,</math> จากนั้นเรียงจุดที่คัดมาจากน้อยไปมากใส่ใน array ชื่อ P ตามแนวแกน y แล้ว ถ้า <math> P[i] \,</math> และ <math> P[j] \,</math> เป็นคู่ที่อยู่ใกล้กันเป็นระยะห่างน้อยกว่า <math> d \,</math> และ <math> i < j \,</math> แล้ว <math> j \leq i + 15 \,</math> | ||
| + | |||
| + | ดังนั้นถ้า สมมติว่าเรียงจุดตามที่กำหนดไว้ข้างต้น หาจุดที่อยู่ใกล้กันเป็นระยะห่างน้อยกว่า <math> d' \, </math> ได้ในเวลา <math> 15n \, </math> | ||
| + | |||
| + | |||
| + | Closet_Pairs(p,n) | ||
| + | : if n <= 1 | ||
| + | :: return d= \infinity | ||
| + | : else if n = 2 | ||
| + | :: return d(P[0],P[1]) // ระยะทางระหว่างสองจุดนั้น | ||
| + | :else | ||
| + | :: k <-- n/2 // เวลาการทำงานส่วนนี้คือ O(1) | ||
| + | :: L<--(P[0], P[1], P[2], ..., P[k-1]) // เวลาการทำงานส่วนนี้คือ O(n) | ||
| + | :: R<--(P[k], P[k+1], P[k+2], ..., P[n-1]) // เวลาการทำงานส่วนนี้คือ O(n) | ||
| + | :: d_L, P_L[0], P_L[1] <-- Closet_Pair(L, k) // เวลาการทำงานส่วนนี้คือ T(n/2) | ||
| + | :: d_R, P_R[0], P_R[1] <-- Closet_Pair(R, n-k) // เวลาการทำงานส่วนนี้คือ T(n/2) | ||
| + | :: P' <-- Merge(L', R') // ตามแนวแกน y , เวลาการทำงานส่วนนี้คือ O(n) | ||
| + | :: d' <-- min (d_R, d_L) // เวลาการทำงานส่วนนี้คือ O(n) | ||
| + | :: P'' <- จุดใน P' ที่อยู่ในช่วง [x'-d',x'+d'] // เวลาการทำงานส่วนนี้คือ O(n) | ||
| + | :: for i = o to n-16 // loop for นี้มีเวลาการทำงาน O(n) | ||
| + | ::: for j = i to i+15 | ||
| + | :::: if d(P[i],P[j]) < d' // ถ้าระยะห่างระหว่าง P[i] กับ P[j] น้อยกว่า d' | ||
| + | :::: d'<-- d[P[i],P[j]) | ||
| + | : return d', คู่ของจุดที่อยู่ใกล้กันที่สุด, P' | ||
| + | |||
| + | |||
| + | |||
| + | Partition (a, l, r, x) | ||
| + | : k <-- l | ||
| + | : for i=l to r | ||
| + | :: if a[i] <= x | ||
| + | ::: swap(a[i],a[k]) | ||
| + | ::: k <-- k +1 | ||
| + | : return k | ||
| + | |||
| + | |||
| + | Quicksort (a, l, r) | ||
| + | : if r-l+1 <= 1 | ||
| + | :: ไม่ต้องทำอะไร | ||
| + | : else | ||
| + | :: x <-- choose pivot (a, l, r) | ||
| + | :: l <-- partition (a, l, r, x) | ||
| + | :: Quicksort (a, l, k-1) | ||
| + | :: Quicksort (a, k, r) | ||
| + | |||
| + | |||
| + | วิธีการเลือก pivot | ||
| + | :1. เลือกตัวแรก x<-- a[l] | ||
| + | :2. เลือกตัวสุดท้าย x<-- a[r] | ||
| + | :3. tri-median ค่าตัวกลางของ a[l], a[r], a[(l+r)/2] | ||
| + | :4. สุ่ม p<-- random (l, r) | ||
| + | :: x <-- a[p] | ||
| + | |||
| + | |||
| + | ให้ <math> T(n) \, </math> เวลาการทำงานของ Quicksort | ||
| + | เมื่อ <math> r-l+1 = n \, </math> | ||
| + | |||
| + | <math> T(n) = O(1) \, </math> เมื่อ <math> n=1 \, </math> | ||
| + | |||
| + | <math> T(n) = T(k) + T(n-k) + O(n) \, </math> เมื่อ <math> n > 1 \, </math> | ||
| + | |||
| + | |||
| + | พิจารณาเวลาการทำงานกรณีแย่ที่สุด คือแบ่งแล้วได้ด้านหนึ่งมีสมาชิกอยู่หนึ่งตัว แล้วอีกด้านเป็นตัวที่เหลือ (<math> k=1 \, </math> หรือ <math> k=n-1 \,</math>) ดังนั้นเวลาการทำงานจะเป็นดังนี้ | ||
| + | |||
| + | <math> T(n) = O(1) \, </math> เมื่อ <math> n=1 \, </math> | ||
| + | |||
| + | <math> T(n) = T(1) + T(n-1) + O(n) = T(n-1) + O(n) \, </math>เมื่อ <math> n > 1 \, </math> | ||
| + | |||
| + | ซึ่งกรณีนี้ท้ายที่สุดแล้ว <math> T(n) = \Theta (n^2) \, </math> | ||
| + | |||
| + | |||
| + | พิจารณาเวลาการทำงานกรณีดีที่สุด คือแบ่งแล้วได้ครึ่ง ๆ พอดี (<math> k=n/2 \, </math> ดังนั้นเวลาการทำงานจะเป็นดังนี้ | ||
| + | |||
| + | <math> T(n) = O(1) \, </math> เมื่อ <math> n=1 \, </math> | ||
| + | |||
| + | <math> T(n) = 2T(n/2) + O(n) \, </math>เมื่อ <math> n > 1 \, </math> | ||
| + | |||
| + | ซึ่งกรณีนี้ท้ายที่สุดแล้ว <math> T(n) = \Theta(n log n) \, </math> | ||
| + | |||
| + | |||
| + | |||
| + | แต่ถ้าเป็นกรณีสุ่มค่า pivot x แล้ว <math> T(n) \, </math> จะเป็น random variable ดังนั้นเวลาการทำงานจะคิดเป็นกรณีเฉลี่ย คือ <math> E(T(n))= \Theta(n log n)\, </math> | ||
รุ่นแก้ไขปัจจุบันเมื่อ 07:13, 4 กันยายน 2552
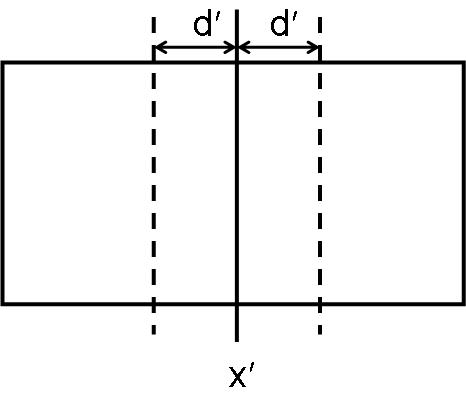
ข้อสังเกต1:ถ้ามีคู่ของจุด คู่ที่อยู่ใกล้กันกว่าระยะทาง หมายความว่า จุดทั้งสองจะต้องอยู่ในแถบ เท่านั้น ดังภาพ
ข้อสังเกต 2: ถ้าสมมติดว่าแบ่งแถบ ออกเป็นช่อง ๆ แต่ละช่องมีความกว้างและความยาวเป็น ดังภาพ
ข้อสังเกต 3: ถ้ามีจุด ที่อยู่ใกล้กัน เป็นระยะห่างน้อยกว่า และจะมีตารางขนาด 4 x 4 ที่แต่ละช่องมีความกว้าง ที่ อยู่ในตารางนั้นเสมอ ดังภาพ
ข้อสังเกต 4: ถ้านำเซต และเซต มารวมกัน แล้วคัดเฉพาะจุดที่อยู่ในแถบ จากนั้นเรียงจุดที่คัดมาจากน้อยไปมากใส่ใน array ชื่อ P ตามแนวแกน y แล้ว ถ้า และ เป็นคู่ที่อยู่ใกล้กันเป็นระยะห่างน้อยกว่า และ แล้ว
ดังนั้นถ้า สมมติว่าเรียงจุดตามที่กำหนดไว้ข้างต้น หาจุดที่อยู่ใกล้กันเป็นระยะห่างน้อยกว่า ได้ในเวลา
Closet_Pairs(p,n)
- if n <= 1
- return d= \infinity
- else if n = 2
- return d(P[0],P[1]) // ระยะทางระหว่างสองจุดนั้น
- else
- k <-- n/2 // เวลาการทำงานส่วนนี้คือ O(1)
- L<--(P[0], P[1], P[2], ..., P[k-1]) // เวลาการทำงานส่วนนี้คือ O(n)
- R<--(P[k], P[k+1], P[k+2], ..., P[n-1]) // เวลาการทำงานส่วนนี้คือ O(n)
- d_L, P_L[0], P_L[1] <-- Closet_Pair(L, k) // เวลาการทำงานส่วนนี้คือ T(n/2)
- d_R, P_R[0], P_R[1] <-- Closet_Pair(R, n-k) // เวลาการทำงานส่วนนี้คือ T(n/2)
- P' <-- Merge(L', R') // ตามแนวแกน y , เวลาการทำงานส่วนนี้คือ O(n)
- d' <-- min (d_R, d_L) // เวลาการทำงานส่วนนี้คือ O(n)
- P <- จุดใน P' ที่อยู่ในช่วง [x'-d',x'+d'] // เวลาการทำงานส่วนนี้คือ O(n)
- for i = o to n-16 // loop for นี้มีเวลาการทำงาน O(n)
- for j = i to i+15
- if d(P[i],P[j]) < d' // ถ้าระยะห่างระหว่าง P[i] กับ P[j] น้อยกว่า d'
- d'<-- d[P[i],P[j])
- for j = i to i+15
- return d', คู่ของจุดที่อยู่ใกล้กันที่สุด, P'
Partition (a, l, r, x)
- k <-- l
- for i=l to r
- if a[i] <= x
- swap(a[i],a[k])
- k <-- k +1
- if a[i] <= x
- return k
Quicksort (a, l, r)
- if r-l+1 <= 1
- ไม่ต้องทำอะไร
- else
- x <-- choose pivot (a, l, r)
- l <-- partition (a, l, r, x)
- Quicksort (a, l, k-1)
- Quicksort (a, k, r)
วิธีการเลือก pivot
- 1. เลือกตัวแรก x<-- a[l]
- 2. เลือกตัวสุดท้าย x<-- a[r]
- 3. tri-median ค่าตัวกลางของ a[l], a[r], a[(l+r)/2]
- 4. สุ่ม p<-- random (l, r)
- x <-- a[p]
ให้ เวลาการทำงานของ Quicksort
เมื่อ
เมื่อ
เมื่อ
พิจารณาเวลาการทำงานกรณีแย่ที่สุด คือแบ่งแล้วได้ด้านหนึ่งมีสมาชิกอยู่หนึ่งตัว แล้วอีกด้านเป็นตัวที่เหลือ ( หรือ ) ดังนั้นเวลาการทำงานจะเป็นดังนี้
เมื่อ
เมื่อ
ซึ่งกรณีนี้ท้ายที่สุดแล้ว
พิจารณาเวลาการทำงานกรณีดีที่สุด คือแบ่งแล้วได้ครึ่ง ๆ พอดี ( ดังนั้นเวลาการทำงานจะเป็นดังนี้
เมื่อ
เมื่อ
ซึ่งกรณีนี้ท้ายที่สุดแล้ว
แต่ถ้าเป็นกรณีสุ่มค่า pivot x แล้ว จะเป็น random variable ดังนั้นเวลาการทำงานจะคิดเป็นกรณีเฉลี่ย คือ


![{\displaystyle [x'-d',x'+d']\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ff7197814178406bd3c7682bc2f803f9e5ea454)




![{\displaystyle P[i]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d8e98f6e7843a41220b66ec4a2034f5fa24abe)
![{\displaystyle P[j]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be2ea384aeeec35c34b6fb4413b064e9ddfc86d6)

















