ผลต่างระหว่างรุ่นของ "204512-53/lecture4"
| แถว 23: | แถว 23: | ||
*จำนวนลูกบอลในถังที่มีจำนวนมากที่สุด | *จำนวนลูกบอลในถังที่มีจำนวนมากที่สุด | ||
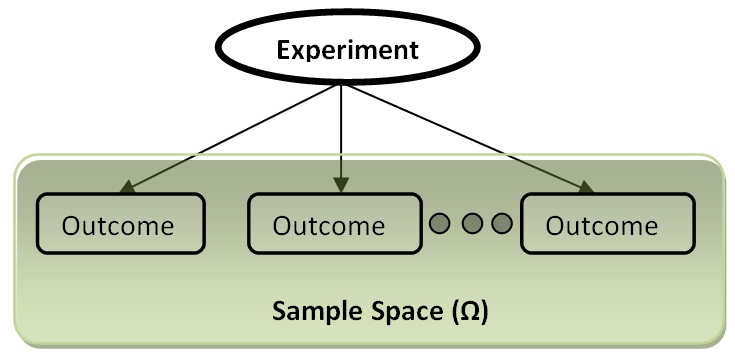
ในการเรียนความน่าจะเป็น หรือการทดลองแบบสุ่มจำเป็นต้องเข้าใจ ศัพท์ต่างๆ ดังนี้ Random experiment คือการทดลองแบบสุ่ม ซึ่งจะได้ผลลัพธ์ออกมาคือ outcome outcome เป็นสิ่งที่สังเกตได้ ซึ่งในการทดลองแต่ละครั้งก็จะได้ outcome ออกมาหลายๆ อัน เซตของ outcome ทั้งหมดที่เป็นไปได้ เรียกว่า sample space ตามภาพด้านล่าง | ในการเรียนความน่าจะเป็น หรือการทดลองแบบสุ่มจำเป็นต้องเข้าใจ ศัพท์ต่างๆ ดังนี้ Random experiment คือการทดลองแบบสุ่ม ซึ่งจะได้ผลลัพธ์ออกมาคือ outcome outcome เป็นสิ่งที่สังเกตได้ ซึ่งในการทดลองแต่ละครั้งก็จะได้ outcome ออกมาหลายๆ อัน เซตของ outcome ทั้งหมดที่เป็นไปได้ เรียกว่า sample space ตามภาพด้านล่าง | ||
| − | [[ไฟล์:2553w04_ball&bin01.jpg|center| | + | [[ไฟล์:2553w04_ball&bin01.jpg|center|400px|]] |
| + | ปกติเราไม่ได้สนใจไปที่ outcome โดยแท้จริง เพราะ outcome มีอยู่ได้เยอะแยะ บางครั้งเราสนใจคุณสมบัติบางอย่างของ outcome เช่น<br /> | ||
| + | นิยาม experiment ในกรณี ball and bin มีถัง n ถังลูกบอล m ลูก ลูกบอลแต่ละลูกโยนเป็นอิสระต่อกัน ความน่าจะเป็นที่ลูกบอลแต่ละลูกลงถังๆ หนึ่งคือ 1/n<br /> | ||
| + | จากการทดลองก็จะได้ว่าลูกบอลลูกที่ 1 ลงถังไหน ลูกบอลลูกที่ 2 ลงถังไหน… ซึ่ง Outcome ของเราขึ้นอยู่กับว่าความสังเกตได้ของเรา เช่นถ้าลูกบอลที่ 1 กับ 5 มีลักษณะเหมือนกัน แยกกันไม่ออก เซตของ outcome ก็จะเปลี่ยนไป sample space ก็จะเปลี่ยนไป แต่ถ้าการทดลองเรื่องเดียวกัน experiment วัดแบบเดียวกัน มันต้องได้ออกมาเหมือนกัน<br /> | ||
| + | จากการทดลองเราไม่ได้สนใจที่ outcome โดยแท้จริงแต่เราสนใจคุณสมบัติบางอย่างเช่น<br /> | ||
| + | *จำนวนถังที่มีลูกบอลมากว่า 1 ลูก | ||
| + | *จำนวนถังว่าง | ||
| + | *จำนวนลูกบอลในถังที่มากที่สุด | ||
| + | ซึ่งค่าเหล่านี้ถ้าไม่ทดลองจะไม่รู้ค่า เราจะรู้ค่าก็ต่อเมื่อเราทดลองเสร็จแล้วหรือเรามี outcome ออกมาแล้ว ค่าตรงนี้เปลี่ยนแปลงไปตามผลลัพธ์การทดลอง เราจะเรียกค่าตรงนี้หรือผลลัพธ์เหล่านี้ว่า random variable (ตัวแปรสุ่ม) ก็คือตัวแปรที่มีค่าเปลี่ยนแปลงไปตามผลลัพธ์ แต่ในความหมายหนึ่งในเชิงทางการแล้ว random variable เป็นฟังก์ชันจาก sample space ไปอะไรบางอย่าง Ω → R (มีค่าเป็นจำนวนจริง) เช่นจำนวนถังที่ว่าง ได้ outcome แล้วสามารถบอกได้เลยว่ามีถังว่างกี่อัน ถ้าไม่มี outcome ก็ไม่สามารถบอกได้ว่ามีถังว่างกี่อัน<br /> | ||
รุ่นแก้ไขเมื่อ 17:25, 9 สิงหาคม 2553
บันทึกคำบรรยายวิชา 204512-53 นี้ เป็นบันทึกที่นิสิตเขียนขึ้น เนื้อหาโดยมากยังไม่ผ่านการตรวจสอบอย่างละเอียด การนำไปใช้ควรระมัดระวัง
จดบันทึกคำบรรยายโดย:
นายกฤตกรณ์ ศรีวันนา G5314550024 นายณัฐพล จารุพัฒนะสิริกุล G5314550067 นายพงศกร สุระธรรม G5314550130 นายวุฒิชัย วภักดิ์เพชร G5314550181
Hashing
มี key กับ value K ∈{0,1,…,M-1} M มีค่าเยอะมากๆ ปกติแล้วถ้ามีข้อมูล n ตัว จะใช้ array เก็บ n ช่อง หรือ cn ช่อง (เมื่อ c เป็นค่าคงที่) ให้ m เป็นขนาดของ array หรือขนาดของ table ซึ้ง m >= n
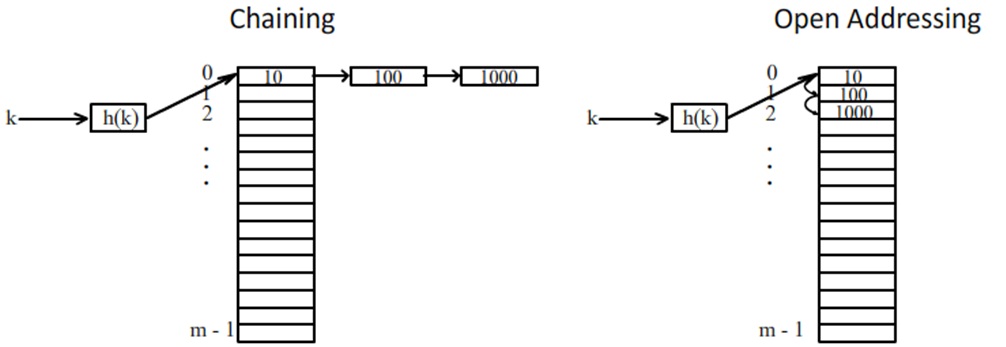
มี hash function h ที่รับ k เข้าไปแล้วทำการ map ไป space ของ table(0,1,…,m-1) เมื่อเรารู้ค่า key เราก็จะรู้ว่าจะไปหาข้อมูลที่ ช่องไหน ถ้าข้อมูลที่แตกต่างกันลงกันคนละช่อง table ก็เปรียบเป็น array นั้นเอง เรื่องที่สนในการทำ Hashing มีสองเรื่องคือ 1. วิธีหรือฟังก์ชันที่ใช้ในการคำนวณหาค่าที่ตำแหน่งที่ใช้เก็บข้อมูล 2. การแก้ปัญหาเมื่อเกิดการชนกันเกิดขึ้น ตัวอย่างการแก้ปัญหาเมื่อเกิดการชนกันคือ การใช้วิธี chaining ในการแก้ปัญหาการชนกันโดยการใช้ link list มาใช้เก็บข้อมูลที่ชนกันตามภาพด้านล้าง หรือแก้โดยวิธี open addressing คือข้อมูลที่ชนกันจะถูกเก็บลงในช่องถัดไปที่ว่าง ตามภาพด้านล้างการวิเคราะห์ปัญหาการใช้ hash สิ่งแรกคือ วิเคราะห์ว่า hash function นั้นดี ซึ่งมีอยู่จริงแต่อาจไม่ดีสำหรับสำหรับทุกๆ input สำหรับ hash function ที่ดีนั้นควรจะมีการสุ่มแบบกระจาย สำหรับการวิเคราะห์จะอาศัยการวิเคราะห์ของการทดลองตระกูล Ball and Bin
Ball and Bin
มีถัง n ถัง ลูกบอล m ลูก โยนลูกบอลไปสุ่มๆ ลงถังไหนก็ได้ด้วยความน่าจะเป็นที่เท่ากัน สิ่งที่สนใจคือ
- ถังที่มีลูกบอลมากกว่า 1 ลูก
- จำนวนถังว่าง
- จำนวนลูกบอลในถังที่มีจำนวนมากที่สุด
ในการเรียนความน่าจะเป็น หรือการทดลองแบบสุ่มจำเป็นต้องเข้าใจ ศัพท์ต่างๆ ดังนี้ Random experiment คือการทดลองแบบสุ่ม ซึ่งจะได้ผลลัพธ์ออกมาคือ outcome outcome เป็นสิ่งที่สังเกตได้ ซึ่งในการทดลองแต่ละครั้งก็จะได้ outcome ออกมาหลายๆ อัน เซตของ outcome ทั้งหมดที่เป็นไปได้ เรียกว่า sample space ตามภาพด้านล่าง
ปกติเราไม่ได้สนใจไปที่ outcome โดยแท้จริง เพราะ outcome มีอยู่ได้เยอะแยะ บางครั้งเราสนใจคุณสมบัติบางอย่างของ outcome เช่น
นิยาม experiment ในกรณี ball and bin มีถัง n ถังลูกบอล m ลูก ลูกบอลแต่ละลูกโยนเป็นอิสระต่อกัน ความน่าจะเป็นที่ลูกบอลแต่ละลูกลงถังๆ หนึ่งคือ 1/n
จากการทดลองก็จะได้ว่าลูกบอลลูกที่ 1 ลงถังไหน ลูกบอลลูกที่ 2 ลงถังไหน… ซึ่ง Outcome ของเราขึ้นอยู่กับว่าความสังเกตได้ของเรา เช่นถ้าลูกบอลที่ 1 กับ 5 มีลักษณะเหมือนกัน แยกกันไม่ออก เซตของ outcome ก็จะเปลี่ยนไป sample space ก็จะเปลี่ยนไป แต่ถ้าการทดลองเรื่องเดียวกัน experiment วัดแบบเดียวกัน มันต้องได้ออกมาเหมือนกัน
จากการทดลองเราไม่ได้สนใจที่ outcome โดยแท้จริงแต่เราสนใจคุณสมบัติบางอย่างเช่น
- จำนวนถังที่มีลูกบอลมากว่า 1 ลูก
- จำนวนถังว่าง
- จำนวนลูกบอลในถังที่มากที่สุด
ซึ่งค่าเหล่านี้ถ้าไม่ทดลองจะไม่รู้ค่า เราจะรู้ค่าก็ต่อเมื่อเราทดลองเสร็จแล้วหรือเรามี outcome ออกมาแล้ว ค่าตรงนี้เปลี่ยนแปลงไปตามผลลัพธ์การทดลอง เราจะเรียกค่าตรงนี้หรือผลลัพธ์เหล่านี้ว่า random variable (ตัวแปรสุ่ม) ก็คือตัวแปรที่มีค่าเปลี่ยนแปลงไปตามผลลัพธ์ แต่ในความหมายหนึ่งในเชิงทางการแล้ว random variable เป็นฟังก์ชันจาก sample space ไปอะไรบางอย่าง Ω → R (มีค่าเป็นจำนวนจริง) เช่นจำนวนถังที่ว่าง ได้ outcome แล้วสามารถบอกได้เลยว่ามีถังว่างกี่อัน ถ้าไม่มี outcome ก็ไม่สามารถบอกได้ว่ามีถังว่างกี่อัน