จดบันทึกคำบรรยายโดย:
- นางสาว สุกัลยา เลิศวิวัฒน์สกุล รหัส : 50653955
- นางสาว กมลวรรณ โพธิ์แก้ว รหัส : 50653724
ทบทวน
Primal Linear Programming
- minimize :

- subject to :


หรือเขียนเป็น matrix form ได้
- minimize : C′x
- subject to : Ax ≥ b ; x เป็นเมตริกซ์ขนาด n-dimension
- x ≥ 0
Dual Linear Programming
- maximize :

- subject to :


หรือเขียนเป็น matrix form ได้
- maximize : y′b
- subject to : ATy ≤ c ; y เป็นเมตริกซ์ขนาด m-dimension
- y ≥ 0
ตัวอย่าง 1 - Assigment
โจทย์ - มีงาน n งาน
- มีพนักงาน n คน
- assign งาน j ให้กับพนักงาน i ใช้ cost Cij
- ต้องการ assign งานให้กับพนักงาน โดยที่งาน 1 งานให้พนักงาน 1 คน
- และพนักงาน 1 คนได้งาน 1 งาน
วิธีทำ
- ให้ xij เป็น 1 ถ้า assign งาน j ให้กับ i
- เป็น 0 ถ้าเป็นอื่นๆ
จากโจทย์เราเขียนเป็นสมการได้ว่า
Primal
- minimize :

- subject to :



จะเห็นว่าสมการข้างบนเป็น integer program ซึ่งต้องใช้เวลาในการแก้นาน ฉะนั้นเราจะทำให้เป็น linear program แทน
ฉะนั้นเราจะแก้ subject to เป็น



- จะได้ว่าเป็น relaxed linear program
เขียนเป็น Dual
- maximize :

- subject to :



เมื่อเราแปลง Primal → Dual ; ค่า Max ของค่าที่นำมาแปลง จะไม่เกินค่า Min ของค่าที่ถูกแปลง
ตัวอย่าง 2
โจทย์ จากตัวอย่างที่ 1 ต้องการหา optimal maching?
วิธีทำ
- สามารถทำให้ค่า objective = 15 ได้หรือไม่ ?
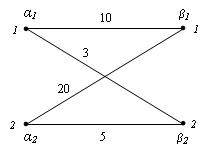
Solution คือ สร้าง Dual ที่มี objective = 15 แล้วสร้าง Primal ที่มี objective = 15 เช่นเดียวกัน
- กำหนดให้
เราจะทำการปรับค่า Dual(feasible แล้ว) ใหม่ แล้วแก้ Primal(infeasible) เก่า ให้เหมาะสมกับ Dual ใหม่ ทำจนกว่าค่าของ Dual และ Primal(feasible ทั้งคู่) จะมีค่าเท่ากัน
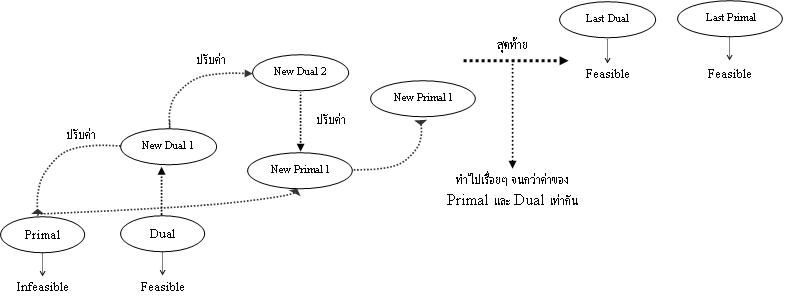
Duality
จาก Prob. priallity
- นิยาม
Primal
- maximize : c′x
- subject to : Ax ≥ b
- x ≥ 0
Dual
- maximize : y′b
- subject to : ATy ≤ c
- y ≥ 0
Weak duality
Thm:
- ถ้า x และ y เป็น feasible solution
- y′b ≤ c′x
Proof:
- y′b ≤ y′Ax ≤ c′x
Storng duality
Thm:
- ถ้า x* และ y* เป็น 2optimal solution ของ PLP, DLP
- c′x* = b′y*
Complementary Slackness
Dual:
- maximize : y′b
- ATy + s = c ; s เป็น matrix ขนาด n มิติเท่า y
- y ≥ 0
- s ≥ 0
Proof:
- (ATy*′ + s)x* = y*′b
- y*′Ax + sx* = y*′b
- y*′b + sx*′ = y*′b
- sx* = 0

ตัวอย่าง 3 : Shortest path
โจทย์ หา shortest path จาก s
วิธีทำ
- ให้กราฟ G = (V,E), l(u,v) แทนความยาวเส้นเชื่อม (u,v)
- ตัวแปร Dv แทนระยะทาง s ไปยัง v
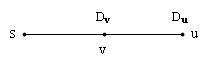
Primal
- maximize :
- Dt - Ds
- subject to :



จะเห็นว่าสมการข้างบนดูยาก เราจะเขียนใหม่ได้
- maximize :
- Dt - Ds
- subject to :


เขียนเป็น Dual ได้
- minimize :
 เป็น cost ของ flow
เป็น cost ของ flow
- subject to :

 flow เข้ามา t 1 หน่วย
flow เข้ามา t 1 หน่วย flow ออกจาก s 1 หน่วย
flow ออกจาก s 1 หน่วย
นี่คือ Dual Program ของ Shortest Path และเป็น form หนึ่งของปัญหา min cost flow
Min-cost Maximun flow
- min-cost flow คือการหา flow ที่มี cost ต่ำที่สุด
- ให้กราฟ G = (V,E)
- capacity u(x,y) บน edge (x,y)
- cost c(x,y) บน edge (x,y)
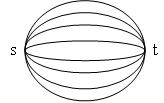 ที่มี cost = ค่าต่ำสุด (route มากสุด = max flow)
ที่มี cost = ค่าต่ำสุด (route มากสุด = max flow)
- min-cost circulation คือ flow = 0 โดยหมุนวนใน flow. จากรูป
- minimize :

- subject to :
 (flow เข้า = flow ออก)
(flow เข้า = flow ออก)



 ที่มี cost = ค่าต่ำสุด (route มากสุด = max flow)
ที่มี cost = ค่าต่ำสุด (route มากสุด = max flow)































